Question

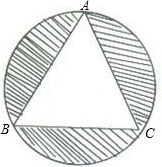
（1）如图1，已知△PAC是圆O的内接正三角形，那么∠OAC﹦______；
（2）如图2，设AB是圆O的直径，AC是圆的任意一条弦，∠OAC﹦α﹒
①如果α﹦45°，那么AC能否成为圆内接正多边形的一条边？若有可能，那么此多边形是几边形？请说明理由﹒
②若AC是圆的内接正n边形的一边，则用含n的代数式表示α应为______﹒

Answer 1

（1）∵△PAC是圆O的内接正三角形，
∴∠AOC=2∠APC=2×60°=120°，
∵OA=OC，
∴∠OAC=

180°-∠AOC

2

=

180°-120°

2

=30°；

（2）①能﹒
∵α=45°，
∴圆内接正多边形的一个内角为90°，
∴是正方形﹒
②∵AC是圆的内接正n边形的一边，
∴2α=

(n-2)×180°

n

，
∴α=90°-

180°

n

．