题目内容
半径是2和3的两圆交于M、N两点，过交点分别作各圆的切线且相互经过另一个圆的圆心，则公共弦MN之长为（ ）
| A．6 | B．12 | C．
| D．
|
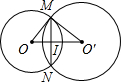
如图所示：连接MN，
∵过交点M，N分别作各圆的切线且相互经过另一个圆的圆心，
∴OM⊥O′M，
∵MO=2，MO′=3，
∴OO′=
=
，
由题意可得：OO′⊥MN，MI=IN，
∴MI•OO′=MO•MO′，
∴MI=
=
=
，
∴MN=2×
=
．
故选：C．
∵过交点M，N分别作各圆的切线且相互经过另一个圆的圆心，
∴OM⊥O′M，
∵MO=2，MO′=3，
∴OO′=
| 4+9 |
| 13 |
由题意可得：OO′⊥MN，MI=IN，
∴MI•OO′=MO•MO′，
∴MI=
| MO•MO′ |
| OO′ |
| 2×3 | ||
|
6
| ||
| 13 |
∴MN=2×
6
| ||
| 13 |
12
| ||
| 13 |
故选：C．
练习册系列答案
阅读快车系列答案
相关题目
