题目内容
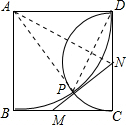
如图，ABCD是边长为a的正方形，以A为圆心，AD为半径的圆弧与以CD为直径的半圆交于另一点P，过P作⊙A的切线分别交BC、CD于M、N两点，则
=______．
| PM |
| PN |
如图，连接AN、DP、AP．
∵AP=AD，
∴△APD是等腰三角形；
又∵MN是⊙A的切线，AD⊥DN，
∴∠PAN=∠DAN；
∴AN⊥PD；
而点A圆心，N在连心线上，
∴点N是圆心，
∴ND=NC=
；
∵MN是⊙A的切线，AB⊥BM，
∴BM=PM；
同理，DN=PN；
∴在直角三角形MNC中，（PM+PN）2=CM2+CN2，即（BM+
）2=（a-BM）2+（
）2，
解得，BM=
，
∴
=
=
=
；
故答案是：
．
∵AP=AD，
∴△APD是等腰三角形；
又∵MN是⊙A的切线，AD⊥DN，
∴∠PAN=∠DAN；
∴AN⊥PD；
而点A圆心，N在连心线上，
∴点N是圆心，
∴ND=NC=
| a |
| 2 |
∵MN是⊙A的切线，AB⊥BM，
∴BM=PM；
同理，DN=PN；
∴在直角三角形MNC中，（PM+PN）2=CM2+CN2，即（BM+
| a |
| 2 |
| a |
| 2 |
解得，BM=
| a |
| 3 |
∴
| PM |
| PN |
| BM |
| DN |
| ||
|
| 2 |
| 3 |
故答案是：
| 2 |
| 3 |
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
