题目内容
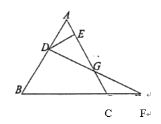
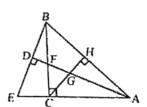
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,与BC相交于点F,过点B作BE⊥AD于点D,交AC延长线于点E,过点C作CH⊥AB于点H,交AF于点G,则下列结论:![]() ⑤
⑤![]() ;正确的有( )个.
;正确的有( )个.
A.1B.2C.3D.4
【答案】D
【解析】
①②正确,只要证明△BCE≌△ACF,△ADB≌△ADE即可解决问题;
③正确,只要证明GB=GA,得到△BDG是等腰直角三角形,即可得到;
④正确,求出∠CGF=67.5°=∠CFG,则CF=CG=CE,然后AE=AC+CE=BC+CG,即可得到结论;
⑤错误,作GM⊥AC于M.利用角平分线的性质定理即可证明;
解:∵AD⊥BE,
∴∠FDB=∠FCA=90°,
∵∠BFD=∠AFC,
∴∠DBF=∠FAC,
∵∠BCE=∠ACF=90°,BC=AC,
∴△BCE≌△ACF,
∴EC=CF,AF=BE,故①正确,
∵∠DAB=∠DAE,AD=AD,∠ADB=∠ADE=90°,
∴△ADB≌△ADE,
∴BD=DE,
∴AF=BE=2BD,故②正确,
如图,连接BG,
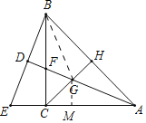
∵CH⊥AB,AC=AB,
∴BH=AH,∠BHG=∠AHG=90°
∵HG=HG,
∴△AGH≌△BGH,
∴BG=AG,∠GAH=∠GBH=22.5°,
∴∠DGB=∠GAH+∠GBH=45°,
∴△BDG是等腰直角三角形,
∴BD=DG=DE;故③正确;
由△ACH是等腰直角三角形,
∴∠ACG=45°,
∴∠CGF=45°+22.5°=67.5°,
∵∠CFG=∠DFB=90°-22.5°=67.5°,
∴∠CGF=∠CFG,
∴CG=CF,
∵AB=AE,BC=AC,CE=CF=CG,
又∵AE=AC+CE,
∴AB=BC+CG,故④正确;
作GM⊥AC于M,

由角平分线性质,GH=GM,
∴△AGH≌△AGM(HL),
∴△AGH的面积与△AGM的面积相等,
故⑤错误;
综合上述,正确的结论有:①②③④;
故选择:D.

 考前必练系列答案
考前必练系列答案