题目内容
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.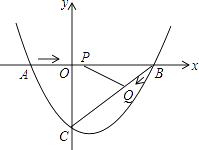
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标.
【答案】
(1)解:把点A(﹣2,0)、B(4,0)分别代入y=ax2+bx﹣3(a≠0),得
![]() ,
,
解得 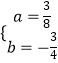 ,
,
所以该抛物线的解析式为:y= ![]() x2﹣
x2﹣ ![]() x﹣3;
x﹣3;
(2)解:设运动时间为t秒,则AP=3t,BQ=t.
∴PB=6﹣3t.
由题意得,点C的坐标为(0,﹣3).
在Rt△BOC中,BC= ![]() =5.
=5.
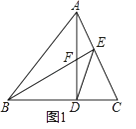
如图1,过点Q作QH⊥AB于点H.
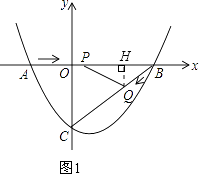
∴QH∥CO,
∴△BHQ∽△BOC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴HQ= ![]() t.
t.
∴S△PBQ= ![]() PBHQ=
PBHQ= ![]() (6﹣3t)
(6﹣3t) ![]() t=﹣
t=﹣ ![]() t2+
t2+ ![]() t=﹣
t=﹣ ![]() (t﹣1)2+
(t﹣1)2+ ![]() .
.
当△PBQ存在时,0<t<2
∴当t=1时,
S△PBQ最大= ![]() .
.
答:运动1秒使△PBQ的面积最大,最大面积是 ![]() ;
;
(3)解:设直线BC的解析式为y=kx+c(k≠0).
把B(4,0),C(0,﹣3)代入,得
![]() ,
,
解得 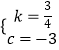 ,
,
∴直线BC的解析式为y= ![]() x﹣3.
x﹣3.
∵点K在抛物线上.
∴设点K的坐标为(m, ![]() m2﹣
m2﹣ ![]() m﹣3).
m﹣3).
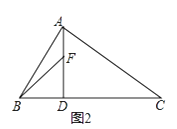
如图2,过点K作KE∥y轴,交BC于点E.则点E的坐标为(m, ![]() m﹣3).
m﹣3).
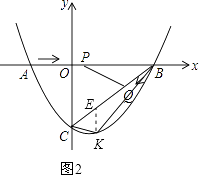
∴EK= ![]() m﹣3﹣(
m﹣3﹣( ![]() m2﹣
m2﹣ ![]() m﹣3)=﹣
m﹣3)=﹣ ![]() m2+
m2+ ![]() m.
m.
当△PBQ的面积最大时,∵S△CBK:S△PBQ=5:2,S△PBQ= ![]() .
.
∴S△CBK= ![]() .
.
S△CBK=S△CEK+S△BEK= ![]() EKm+
EKm+ ![]() EK(4﹣m)
EK(4﹣m)
= ![]() ×4EK
×4EK
=2(﹣ ![]() m2+
m2+ ![]() m)
m)
=﹣ ![]() m2+3m.
m2+3m.
即:﹣ ![]() m2+3m=
m2+3m= ![]() .
.
解得 m1=1,m2=3.
∴K1(1,﹣ ![]() ),K2(3,﹣
),K2(3,﹣ ![]() ).
).
【解析】方法二:(1)略.(2)设运动时间为t秒,则AP=3t,BQ=t,PB=6﹣3t,
∴点C的坐标为(0,﹣3),
∵B(4,0),∴lBC:y= ![]() x﹣3,
x﹣3,
过点Q作QH⊥AB于点H,
∴tan∠HBQ= ![]() ,∴sin∠HBQ=
,∴sin∠HBQ= ![]() ,
,
∵BQ=t,∴HQ= ![]() t,
t,
∴S△PBQ= ![]() PBHQ=
PBHQ= ![]() =﹣
=﹣ ![]() ,
,
∴当t=1时,S△PBQ最大= ![]() .
.
⑶过点K作KE⊥x轴交BC于点E,
∵S△CBK:S△PBQ=5:2,S△PBQ= ![]() ,
,
∴S△CBK= ![]() ,
,
设E(m, ![]() m﹣3),K(m,
m﹣3),K(m, ![]() ),
),
S△CBK= ![]() =
= ![]() =﹣
=﹣ ![]() ,
,
∴﹣ ![]() =
= ![]() ,
,
∴m1=1,m2=3,
∴K1(1,﹣ ![]() ),K2(3,﹣
),K2(3,﹣ ![]() ).
).