题目内容
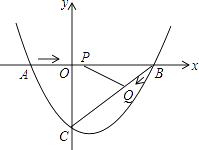
【题目】如图AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PC=2PB.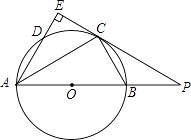
(1)探究线段PB,AB之间的数量关系,并说明理由;
(2)若AD=3,求AB长.
【答案】
(1)解:线段PB,AB之间的数量关系为:AB=3PB.
理由:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC+∠ABC=90°,
∵OB=OC,
∴∠OCB=∠ABC,
∵∠PCB+∠OCB=90°,
∴∠PCB=∠PAC,
∵∠P是公共角,
∴△PCB∽△PAC,
∴ ![]() =
= ![]() ,
,
∴PC2=PBPA,
∵PB:PC=1:2,
∴PC=2PB,
∴PA=4PB,
∴AB=3PB;
(2)解:过点O作OH⊥AD于点H,则AH= ![]() AD=
AD= ![]() ,四边形OCEH是矩形,
,四边形OCEH是矩形,
∴OC=HE,
∴AE= ![]() +OC,
+OC,
∵OC∥AE,
∴△PCO∽△PEA,
∴ ![]() =
= ![]() ,
,
∵AB=3PB,AB=2OB,
∴OB= ![]() PB,
PB,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴OC= ![]() ,
,
∴AB=5,
【解析】(1)利用切线性质定理可证出∠PCB=∠PAC,再加上∠P是公共角,得出△PCB∽△PAC,对应边成比例可得出PA=4PB,即AB=3PB;(2)证出△PCO∽△PEA,得出对应边成比例,求出半径OC=2.5,进而求出直径AB=5.
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

 优学名师名题系列答案
优学名师名题系列答案【题目】某中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
跳绳数/个 | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
人 数 | 1 | 2 | 8 | 11 | 5 |
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).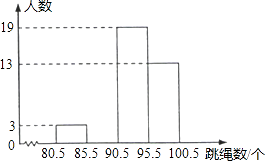
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次跳绳成绩的众数是个,中位数是个;
(3)若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.