题目内容
【题目】已知, 四边形![]() , 连接
, 连接![]() ,
,![]() ,
,![]() .
.
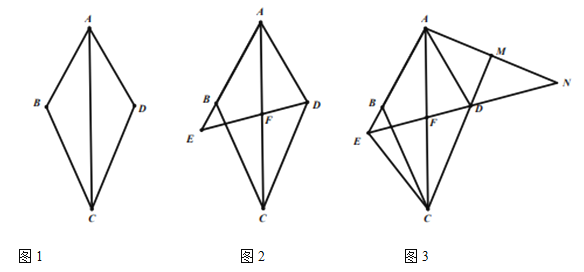
(1)如图![]() , 求证:
, 求证:![]() 平分
平分![]() ;
;
(2)如图![]() ,点
,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
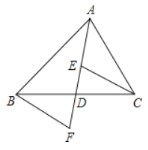
(3)如图3,在![]() 的条件下,连接
的条件下,连接![]() ,点
,点![]() 在
在![]() 延长线上,连接
延长线上,连接![]() ,延长
,延长![]() 与
与![]() 延长线交于点
延长线交于点![]() , 若
, 若![]() ,
,![]() ,
, ![]() 的面积与
的面积与![]() 的面积比为
的面积比为![]() ,
, ![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)根据“SSS”可证△ABC≌△ADC,进而可得∠BAC=∠DAC,由此即可得证;
(2)过点F作FP⊥AB,FQ⊥AD,根据角平分线的性质可得FP=FQ,进而根据S△AEF:S△ADF=AE:AD=EF:DF即可得证;
(3)先根据![]() ,
,![]() 及
及![]() 可证得
可证得![]() ,再根据△EFC和△AFN的内角和可证得
,再根据△EFC和△AFN的内角和可证得![]() ,进而可证得
,进而可证得![]() ,再根据
,再根据![]() 的面积与
的面积与![]() 的面积比为
的面积比为![]() 结合
结合![]() 可求得DN=AD=3,最后根据及求得FD的长,进而可求得FN的长.
可求得DN=AD=3,最后根据及求得FD的长,进而可求得FN的长.
(1)证明:在△ABC与△ADC中,
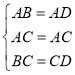
∴△ABC≌△ADC(SSS)
∴∠BAC=∠DAC,
∴![]() 平分
平分![]() ;
;
(2)证明:如图,过点F作FP⊥AB,FQ⊥AD,垂足分别为点P、Q,
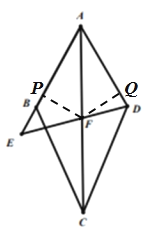
∵![]() 平分
平分![]() ,FP⊥AB,FQ⊥AD,
,FP⊥AB,FQ⊥AD,
∴FP=FQ,
∴S△AEF:S△ADF=![]() AE·FP:
AE·FP:![]() AD·FQ= AE:AD,
AD·FQ= AE:AD,
设点A到DE的距离为h,
则S△AEF:S△ADF=![]() EF·h:
EF·h:![]() FD·h=EF:FD,
FD·h=EF:FD,
∴AE:AD=EF:FD;
(3)解:∵![]() ,
,
∴![]() ,
,
∵![]()
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
且![]() ,
,
∴![]()
∴![]()
∴![]()
∵![]() 的面积与
的面积与![]() 的面积比为
的面积比为![]()
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
∵![]() ,
,![]()
∴![]()
![]()
![]() ,
,
∴![]()
![]()
![]() .
.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目