题目内容
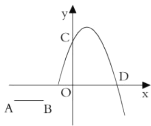
【题目】如图,在△ABC中,以AB为直径的⊙O交BC于点D,交AC于点E,连结DE,且BD=DE,过点B作BP∥DE,交⊙O于点P,连结OP.
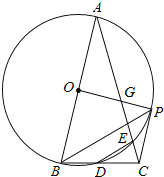
(1)求证:AB=AC;
(2)若∠A=30°,求∠BOP的度数.
【答案】(1)见解析;(2)∠BOP=90°
【解析】
(1)连结AD,根据直径所对的圆周角为直角得到∠ADB=90°,求出∠BAD=∠CAD,△ADB≌△ADC即可;
(2)根据等腰三角形的性质和三角形内角和定理可计算出∠ABC=75°,再根据圆内接四边形的性质得到∠EDC=∠BAC=30°,然后利用平行线的性质得到∠PBC=∠EDC=30°,所以∠OBP=∠ABC-∠PBC=45°,于是可判断△OBP为等腰直角三角形,则∠BOP=90°.
(1)证明:连接AD,
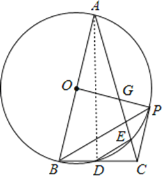
∵BD=DE,
∴![]()
∴∠BAD=∠CAD,
∵AB为⊙O的直径,
∴∠ADB=90°=∠CDA,
在△ADB和△ADC中
∴△ADB≌△ADC(ASA),
∵AB=AC;
(2)解:∵∠BAC=30°,AB=AC,
∴∠ABC=![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∵四边形ABDE为圆O的内接四边形,
∴∠EDC=∠BAC=30°,
∵BP∥DE,
∴∠PBC=∠EDC=30°,
∴∠OBP=∠ABC﹣∠PBC=45°,
∵OB=OP,
∴△OBP为等腰直角三角形,
∴∠BOP=90°.

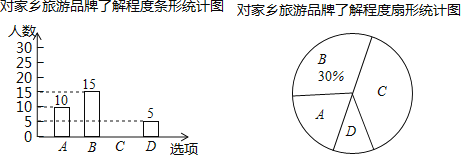
【题目】《中国汉字听写大会》 唤醒了很多人对文字基本功的重视和对汉字文化的学习,某校组织了一次全校2000名学生参加的“汉字听写大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩![]() 取整数,总分100分)作为样本进行整理,得到下列统计图表:
取整数,总分100分)作为样本进行整理,得到下列统计图表:
抽取的200名学生海选成绩分组表
组别 | 海选成绩 |
A组 |
|
B组 |
|
C组 |
|
D组 |
|
E组 |
|

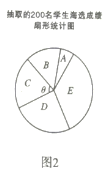
请根据所给信息,解答下列问题
(1)请把图1中的条形统计图补充完整;
(2)在图2的扇形统计图中,表示![]() 组扇形的圆心角
组扇形的圆心角![]() 的度数为_______度;
的度数为_______度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人;
(4)经过统计发现,在![]() 组中,有2位男生和2位女生获得了满分,如果从这4人中挑选2人代表学校参加比赛,请用树状图或列表法求出所选两人正好是一男一女的概率是多少?
组中,有2位男生和2位女生获得了满分,如果从这4人中挑选2人代表学校参加比赛,请用树状图或列表法求出所选两人正好是一男一女的概率是多少?
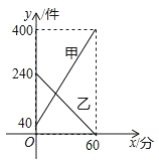
【题目】某种型号的电热水器工作过程如下:在接通电源以后,从初始温度20![]() 下加热水箱中的水,当水温达到设定温度60
下加热水箱中的水,当水温达到设定温度60![]() 时,加热停止;此后水箱中的水温开始逐渐下降,当下降到保温温度30
时,加热停止;此后水箱中的水温开始逐渐下降,当下降到保温温度30![]() 时,再次自动加热水箱中的水至60
时,再次自动加热水箱中的水至60![]() ,加热停止;当水箱中的水温下降到30
,加热停止;当水箱中的水温下降到30![]() 时,再次自动加热,……,按照以上方式不断循环.小宇根据学习函数的经验,对该型号电热水器水箱中的水温随时间变化的规律进行了探究,发现水温
时,再次自动加热,……,按照以上方式不断循环.小宇根据学习函数的经验,对该型号电热水器水箱中的水温随时间变化的规律进行了探究,发现水温![]() 是时间
是时间![]() 的函数,其中
的函数,其中![]() (单位:
(单位:![]() )表示水箱中水的温度,
)表示水箱中水的温度,![]() (单位:
(单位:![]() )表示接通电源后的时间.下面是小宇的探究过程,请补充完整:
)表示接通电源后的时间.下面是小宇的探究过程,请补充完整:
(1)小宇记录了从初始温度20![]() 第一次加热至设定温度60
第一次加热至设定温度60![]() ,之后水温冷却至保温温度30
,之后水温冷却至保温温度30![]() 的过程中,
的过程中,![]() 随
随![]() 的变化情况,如下表所示:
的变化情况,如下表所示:
接通电源后的时间 | 0 | 2 | 4 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | … |
水箱中水的温度 | 20 | 30 | 40 | 60 | 51 | 45 | 40 | 36 | 33 | 30 |
①请写出一个符合加热阶段![]() 与
与![]() 关系的函数解析式______________;
关系的函数解析式______________;
②根据该电热水器的工作特点,当第二次加热至设定温度60![]() 时,距离接通电源的时间
时,距离接通电源的时间![]() 为________
为________![]() .
.
(2)根据上述的表格,小宇画出了当![]() 时的函数图象,请根据该电热水器的工作特点,帮他画出当
时的函数图象,请根据该电热水器的工作特点,帮他画出当![]() 时的函数图象.
时的函数图象.
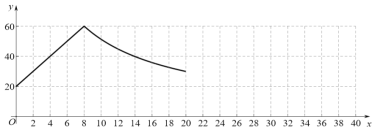
(3)已知适宜人体沐浴的水温约为![]() ,小宇在上午8点整接通电源,水箱中水温为20
,小宇在上午8点整接通电源,水箱中水温为20![]() ,热水器开始按上述模式工作,若不考虑其他因素的影响,请问在上午9点30分时,热水器的水温______(填“是”或“否”)适合他沐浴,理由是_________________.
,热水器开始按上述模式工作,若不考虑其他因素的影响,请问在上午9点30分时,热水器的水温______(填“是”或“否”)适合他沐浴,理由是_________________.