题目内容
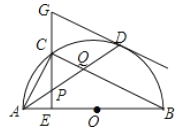
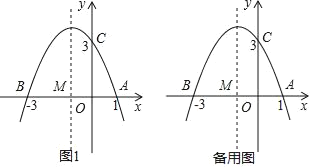
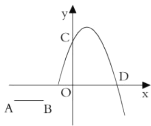
【题目】如图，已知
，线段
与
轴平行，且
，抛物线
经过点
和
，若线段以每秒2个单位长度的速度向下平移，设平移的时间为
（秒）.若抛物线与线段有公共点，则的取值范围是（ ）
A.
B.
C.
D.
【答案】B
【解析】
直接利用待定系数法求出二次函数，得出B点坐标，分别得出当抛物线l经过点B时，当抛物线l经过点A时，求出y的值，进而得出t的取值范围；
解：（1）把点C（0，3）和D（3，0）的坐标代入y=-x2+mx+n中，
得，
解得
∴抛物线l解析式为y=-x2+2x+3，
设点B的坐标为（-2，-1-2t），点A的坐标为（-4，-1-2t），
当抛物线l经过点B时，有y=-（-2）2+2×（-2）+3=-5，
当抛物线l经过点A时，有y=-（-4）2+2×（-4）+3=-21，
当抛物线l与线段AB总有公共点时，有-21≤-1-2t≤-5，
解得：2≤t≤10．
故应选B
练习册系列答案
相关题目
