题目内容
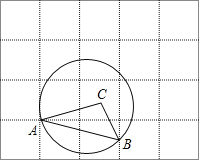
【题目】如图,在每个小正方形的边长为1的网格中,△ABC的顶点A在格点上,B是小正方形边的中点,经过点A,B的圆的圆心在边AC上.
(Ⅰ)弦AB的长等于_____;
(Ⅱ)请用无刻度的直尺,在如图所示的网格中,找出经过出点A,B的圆的圆心O,并简要说明点O的位置是如何找到的(不要求证明)_____.
【答案】![]() 90°的圆周角所对的弦是直径.
90°的圆周角所对的弦是直径.
【解析】
(Ⅰ)根据勾股定理即可得到结论;
(Ⅱ)取圆与网格线的交点D、E,连接DE交AC于O,点O即为经过出点A,B的圆的圆心.
解:(Ⅰ)由勾股定理得:AB=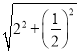 =
=![]() ;
;
故答案为:![]() ;
;
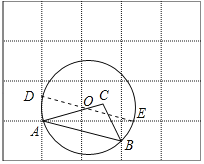
(Ⅱ)如图试所示:取圆与网格线的交点D、E,连接DE交AC于O,点O即为经过出点A,B的圆的圆心;
理由如下:
∵∠EAD=90°,
∴DE为圆O的直径,
∵经过点A,B的圆的圆心在边AC上,
∴DE与AC的交点即为点O;
故答案为:90°的圆周角所对的弦是直径.

练习册系列答案
相关题目