Question

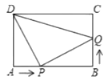
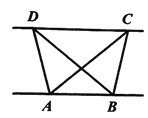
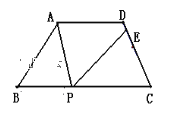
【题目】如图，等腰梯形ABCD中，AD∥BC，AD=3，BC=7，∠B=60°，P为下底BC上一点（不与B、C重合），连结AP，过点P作PE交CD于E，使得∠APE=∠B

（1）求证：△ABP∽△PCE

（2）在底边BC上是否存在一点P，使DE：EC=5：3？如果存在，求BP的长；如果不存在，请说明理由

Answer 1

【答案】（1）见解析（2）1或6

【解析】

（1）由等腰梯形ABCD中，AD∥BC，AB=CD，可得∠B=∠C=60°，又由∠APE+∠EPC=∠B+∠BAP，∠APE=∠B，可证得∠BAP=∠EPC，根据有两角对应相等的三角形相似，即可证得：△APB∽△PEC；

（2）根据DE：EC=5：3，CD=AB=4可得出DE=2.5，EC=1.5．再由△ABP∽△PCE可得出BPPC=6，设BP=x，则x（7-x）=6，求出x的值即可．

解：（1）证明：∵等腰梯形ABCD中，AD∥BC，AB=CD，

∴∠B=∠C=60°，

∵∠APC=∠B+∠BAP，

即∠APE+∠EPC=∠B+∠BAP，

∵∠APE=∠B，

∴∠BAP=∠EPC，

∴△APB∽△PEC；

(2)如图，作AF⊥BC，

则BF=(BCAD)=，

∵∠B=60°，

∴∠BAF=30°，

∴AB=2BF=4；

∵DE:EC=5:3，

∴DE=2.5，EC=1.5.

∵△ABP∽△PCE，

∴AB：PC=BP：CE，

∴4：PC=BP：1.5，

∴BP·PC=6，

设BP=x，则x(7x)=6

解得：x1=1，x2=6；

∴BP的长为：1或6.