题目内容
【题目】如图a,有两个全等的正三角形ABC和DEF,点D、C分别为△ABC、DEF的内心;固定点D,将△DEF顺时针旋转,使得DF经过点C,如图b,则图a中四边形CNDM与图b中△CDM面积的比为( ) 
A.2:1
B.2: ![]()
C.4:3
D.![]() :
: ![]()
【答案】C
【解析】解:如图所示:连接MN、CD. 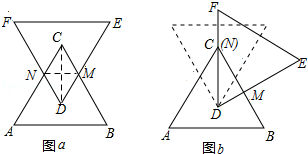
设MN的长为a,CD= ![]() a,则四边形CNDM的面积=
a,则四边形CNDM的面积= ![]() MNCD=
MNCD= ![]() ×a×
×a× ![]() a=
a= ![]() a2 ,
a2 ,
∵∠DCM=30°,∠CDM=60°,
∴DM= ![]() DC=
DC= ![]() ,CM=
,CM= ![]() a.
a.
∴△CDM= ![]() DMCM=
DMCM= ![]() ×
× ![]() ×
× ![]() =
= ![]() a2 .
a2 .
∴四边形CNDM与图b中△CDM面积的比=4:3.
故选;C.
连接MN、CD.由等三角形的性质可知∠DCM=30°,设MN的长为a,CD= ![]() a,由四边形CNDM的面积=
a,由四边形CNDM的面积= ![]() MNCD可求得四边形CNDM的面积,然后在△DCM中,依据特殊锐角三角函数值可求得DM、CM的长,依据三角形的面积公式可求得△CDM的面积,从而可求得答案.
MNCD可求得四边形CNDM的面积,然后在△DCM中,依据特殊锐角三角函数值可求得DM、CM的长,依据三角形的面积公式可求得△CDM的面积,从而可求得答案.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目