题目内容
【题目】一个三角形内有n个点,在这些点及三角形顶点之间用线段连接起来,使得这些线段互不相交,且又能把原三角形分割为不重叠的小三角形.如图:若三角形内有1个点时此时有3个小三角形;若三角形内有2个点时,此时有5个小三角形.则当三角形内有3个点时,此时有个小三角形;当三角形内有n个点时,此时有个小三角形.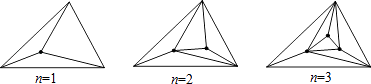
【答案】7;2n+1
【解析】解:观察图形发现有如下规律:
△ABC内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 3 | 5 | 7 | 9 | … | 2n+1 |
∴当三角形内有3个点时,此时有7个小三角形;当三角形内有n个点时,此时有2n+1个小三角形.
故答案为:7,2n+1.
观察图形,不难发现:内部每多一个点,则多2个三角形,则易写出y=3+2(n﹣1);

练习册系列答案
相关题目
【题目】某采摘农场计划种植A,B两种草莓共6亩,根据表格信息,解答下列问题:
项目 品种 | A | B |
年亩产(单位:千克) | 1200 | 2000 |
采摘价格 | 60 | 40 |
(1)若该农场每年草莓全部被采摘的总收入为460000元,那么A、B两种草莓各种多少亩?
(2)若要求种植A种草莓的亩数不少于种植B种草莓的一半,那么种植A种草莓多少亩时,可使该农场每年草莓全部被采摘的总收入最多?并求出最多总收入.