Question

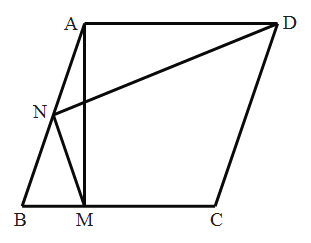
【题目】如图，已知菱形中，，为钝角，于点，为的中点，连接，.若，则过、、三点的外接圆半径为______.

Answer 1

【答案】

【解析】

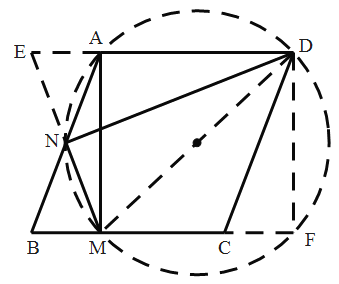
通过延长MN交DA延长线于点E，DF⊥BC,构造全等三角形，根据全等性质证出DE=DM,,再通过AE=BM=CF,在Rt△DMF和Rt△DCF中，利用勾股定理列方程求DM长，根据圆的性质即可求解.

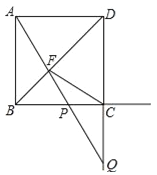
如图，延长MN交DA延长线于点E，过D作DF⊥BC交BC延长线于F,连接MD,

∵四边形ABCD是菱形，

∴AB=BC=CD=4，AD∥BC,

∴∠E=∠EMB, ∠EAN=∠NBM,

∵AN=BN,

∴△EAN≌BMN,

∴AE=BM,EN=MN,

∵,

∴DN⊥EM,

∴DE=DM,

∵AM⊥BC,DF⊥BC,AB=DC,AM=DF

∴△ABM≌△DCF,

∴BM=CF,

设BM=x,则DE=DM=4+x,

在Rt△DMF中，由勾股定理得，DF2=DM2-MF2=(4+x)2-42,

在Rt△DCF中，由勾股定理得，DF2=DC2-CF2=4 2-x2,

∴(4+x)2-42=4 2-x2,

解得，x1=,x2=（不符合题意，舍去）

∴DM=，

∴

∴过、、三点的外接圆的直径为线段DM,

∴其外接圆的半径长为.

故答案为：.