题目内容
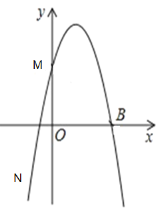
【题目】如图,直线![]() :
:![]() (
(![]() )与
)与![]() ,
,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,以
两点,以![]() 为边在直线
为边在直线![]() 的上方作正方形
的上方作正方形![]() ,反比例函数
,反比例函数![]() 和
和![]() 的图象分别过点
的图象分别过点![]() 和点
和点![]() .若
.若![]() ,则
,则![]() 的值为______.
的值为______.

【答案】-9
【解析】
作CH⊥y轴于点H,证明△BAO≌△CBH,可得OA=BH=-3b,OB=CH=-b,可得点C的坐标为(-b,-2b),点D的坐标为(2b,-3b),代入反比例函数的解析式,即可得出k2的值.
解:如图,作CH⊥y轴于点H,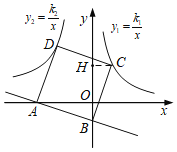
∵四边形ABCD为正方形,
∴AB=BC,∠AOB=∠BHC=90°,∠ABC=90°
∴∠BAO=90°-∠OBA=∠CBH,
∴△BAO≌△CBH(AAS),
∴OA=BH,OB=CH,
∵直线l:![]() (b<0)与x,y轴分别交于A,B两点,
(b<0)与x,y轴分别交于A,B两点,
∴A(3b,0),B(0,b),
∵b<0,
∴BH=-3b,CH=-b,
∴点C的坐标为(-b,-2b),
同理,点D的坐标为(2b,-3b),
∵k1=3,
∴(-b)×(-2b)=3,即2b2=3,
∴k2=2b×(-3b)=-6b2=-9.
故答案为:-9.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目