题目内容
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.
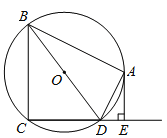
(1)求证:AE是⊙O的切线;
(2)如果AB=4,AE=2,求⊙O的半径.
【答案】
【1】 证明:边结OA,
∵OA=OD,∴∠1=∠2.
∵DA平分![]() ,∴∠2=∠3.
,∴∠2=∠3.
∴∠1=∠3.∴OA∥DE.
∴∠OAE=∠4,[
∵![]() ,∴∠4=90°.∴∠OAE=90°,即OA⊥AE.
,∴∠4=90°.∴∠OAE=90°,即OA⊥AE.
又∵点A在⊙O上,∴AE是⊙O的切线.
【2】 ∵BD是⊙O的直径,∴∠BAD=90°.
∵∠5=90°,∴∠BAD=∠5.
又∵∠2=∠3,∴△BAD∽△AED.∴![]()
∵BA=4,AE=2,∴BD=2AD.
在Rt△BAD中,根据勾股定理,得BD=![]() .
.
∴⊙O半径为![]() .
.
【解析】
试题(1)连接OA,利用已知首先得出OA∥DE,进而证明OA⊥AE就能得到AE是⊙O的切线;
(2)通过证明△BAD∽△AED,再利用对应边成比例关系从而求出⊙O半径的长.
试题解析:(1)连接OA,
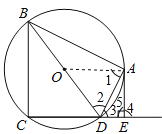
∵OA=OD,
∴∠1=∠2.
∵DA平分∠BDE,
∴∠2=∠3.
∴∠1=∠3.∴OA∥DE.
∴∠OAE=∠4,
∵AE⊥CD,∴∠4=90°.
∴∠OAE=90°,即OA⊥AE.
又∵点A在⊙O上,
∴AE是⊙O的切线.
(2)∵BD是⊙O的直径,
∴∠BAD=90°.
∵∠5=90°,∴∠BAD=∠5.
又∵∠2=∠3,∴△BAD∽△AED.
∴![]() ,
,
∵BA=4,AE=2,∴BD=2AD.
在Rt△BAD中,根据勾股定理,
得BD=![]() .
.
∴⊙O半径为![]() .
.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目