Question

如图，已知：△ABC的外角∠CAG=120°，∠CAG的平分线AD与BC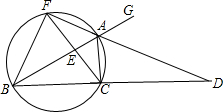的延长线相交于点D，延长DA与．△ABC的外接圆交于点F，连接FB、FC，FC与AB相交于点E．
（1）写出图中除△EFB∽△EAC、△EAF∽△ECB以外的4对相似三角形；
（2）判断△FBC的形状，并说明理由．

Answer 1

（1）∵∠AFC+∠D=60°，∠AFC+∠ACF=60°，
∴∠FCA=∠D．
∵∠AFC=∠CFD，
∴△FAC∽△FCD．
∵∠BAC=∠BCF=60°，∠ABC=∠CBE，
∴△BAC∽△BCE．
∵∠FAE=∠BCE，∠FEA=∠BEC，
∴△FEA∽△BEC，同理△EFB∽△EAC．
∴△FAE∽△BAC．
∵∠FAB=∠BFC=60°，∠FBA=∠EBF，
∴△FBA∽△EBF．
∵∠FAB=∠BAC=60°，∠FBA=∠EAC，
∴△FBA∽△ECA．
同理△DAC∽△DBF．

（2）△FBC为等边三角形，
∵∠CAG=120°，∠CAG的平分线AD与BC的延长线相交于点D，
∴∠GAD=∠DAC=60°，∠CAB=180°-∠GAC=60°．
∴∠BFC=∠BAC=60°，∠BAF=∠GAD=60°．
∴∠BCF=∠BAF=60°．
∴∠FBC=60°．
∴△FBC为等边三角形．