题目内容
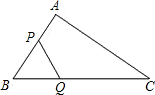
如图，△ABC中，D为AB上一点，在下列四个条件中：
①∠B=∠ACD；②∠ADC=∠ACB；③
=
；④AC2=AD•AB．
能够判定△ABC与△ACD相似的条件是（ ）
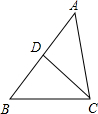
①∠B=∠ACD；②∠ADC=∠ACB；③
| AC |
| CD |
| AB |
| BC |
能够判定△ABC与△ACD相似的条件是（ ）
| A．①②③ | B．①②④ | C．①③④ | D．①②③④ |
∵∠A是公共角，
∴当∠B=∠ACD时，△ABC∽△ACD（有两组角对应相等的两个三角形相似）；
当∠ADC=∠ACB，△ABC∽△ACD（有两组角对应相等的两个三角形相似）；
当
=
时，∠A不是夹角，则不能判定△ABC与△ACD相似；
当AC2=AD•AB时，即
=
，△ABC∽△ACD（两组对应边的比相等且夹角对应相等的两个三角形相似）．
∴能够判定△ABC与△ACD相似的条件是：①②④．
故选B．
∴当∠B=∠ACD时，△ABC∽△ACD（有两组角对应相等的两个三角形相似）；
当∠ADC=∠ACB，△ABC∽△ACD（有两组角对应相等的两个三角形相似）；
当
| AC |
| CD |
| AB |
| BC |
当AC2=AD•AB时，即
| AC |
| AD |
| AB |
| AC |
∴能够判定△ABC与△ACD相似的条件是：①②④．
故选B．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
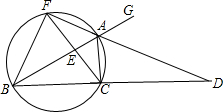的延长线相交于点D，延长DA与．△ABC的外接圆交于点F，连接FB、FC，FC与AB相交于点E．
