题目内容
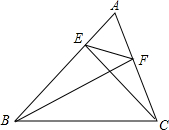
如图，在梯形ABCD中，AD∥BC，AB=AD=CD，点E、F分别在AD、CD边上，且DE=CF，BE与AF相交于点G．找出图中相似的三角形，并证明你所得到结论．
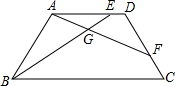
△ABE∽△DAF，△DAF∽△GAE，△ABE∽△GAE，
证明如下：∵在梯形ABCD中，AD∥BC，AB=AD=CD，
∴∠BAD=∠ADC，
∵DE=CF，
∴AE=DF，
∴△ABE≌△DAF，
即△ABE∽△DAF，
∴∠ABE=∠DAF，
∵∠AEB=∠GEA，
∴△ABE∽△GAE，
∴△ADF∽△GAE．
证明如下：∵在梯形ABCD中，AD∥BC，AB=AD=CD，
∴∠BAD=∠ADC，
∵DE=CF，
∴AE=DF，
∴△ABE≌△DAF，
即△ABE∽△DAF，
∴∠ABE=∠DAF，
∵∠AEB=∠GEA，
∴△ABE∽△GAE，
∴△ADF∽△GAE．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
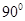，角平分线BE、CF交于点O，则∠BOC =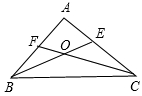 
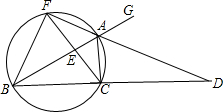的延长线相交于点D，延长DA与．△ABC的外接圆交于点F，连接FB、FC，FC与AB相交于点E．