题目内容
【题目】如图,在△ABC中,AB=14,∠B=45°,tanA=![]() ,点D为AB中点.动点P从点D出发,沿DA方向以每秒1个单位长度的速度向终点A运动,点P关于点D对称点为点Q,以PQ为边向上作正方形PQMN.设点P的运动时间为t秒.
,点D为AB中点.动点P从点D出发,沿DA方向以每秒1个单位长度的速度向终点A运动,点P关于点D对称点为点Q,以PQ为边向上作正方形PQMN.设点P的运动时间为t秒.
(1)当t=______秒时,点N落在AC边上.
(2)设正方形PQMN与△ABC重叠部分面积为S,当点N在△ABC内部时,求S关于t的函数关系式.
(3)当矩形PQMN的对角线所在直线将△ABC的分为面积相等的两部分时,直接写出t的值.
【答案】(1)![]() ;(2)S=
;(2)S= ;(3)t的值为4
;(3)t的值为4![]() -7或7
-7或7![]() -7
-7
【解析】
(1)作CG⊥AB,由∠B=45°可设BG=CG=h,AG=14-h,根据tanA=![]() 求得h=8,再证△APN∽△AGC得
求得h=8,再证△APN∽△AGC得![]() ,据此求解可得;(2)分点M在△ABC内部和外部两种情况:点M在△ABC内部时,重叠部分面积即为正方形的面积;点M在△ABC外部时,重叠部分面积=正方形PQMN的面积-△EMF的面积,据此求解;(3)分直线PM和直线QN将△ABC面积平分的两种情况分别求解可得.
,据此求解可得;(2)分点M在△ABC内部和外部两种情况:点M在△ABC内部时,重叠部分面积即为正方形的面积;点M在△ABC外部时,重叠部分面积=正方形PQMN的面积-△EMF的面积,据此求解;(3)分直线PM和直线QN将△ABC面积平分的两种情况分别求解可得.
(1)如图1,作CG⊥AB于点G,

设BG=h,∵∠B=45°,AB=14,
∴CG=BG=h,AG=14-h,
∵tanA=![]() ,即
,即![]() ,
,
解得:h=8,
则AG=6,
∵DP=DQ=t,
∴PN=PQ=2t,
由PN∥CG知△APN∽△AGC,
∴![]() ,即
,即![]() ,
,
解得:t=![]() ,
,
故答案为:![]() .
.
(2)①如图2,

∵四边形PQMN是正方形,
∴∠BQM=90°,
∵∠B=45°,
∴BQ=MQ,即7-t=2t,
解得t=![]() ,
,
故当0<t≤![]() 时,S=(2t)2=4t2;
时,S=(2t)2=4t2;
②如图3,

∵∠BQF=90°,∠B=45°,
∴BQ=FQ=7-t,∠BFQ=∠MFE=45°,
则MF=MQ-QF=3t-7,
∵∠M=90°,
∴ME=MF=3t-7,
则S=(2t)2-![]() ×(3t-7)2=-
×(3t-7)2=-![]() t2+21t-
t2+21t-![]() (
(![]() <t<
<t<![]() );
);
综上,S= .
.
(3)S△ABC=![]() ABCG=
ABCG=![]() ×14×8=56,
×14×8=56,
①如图4,作HR⊥AB于点R,
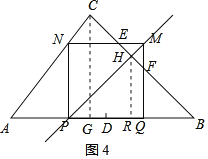
∵四边形PQMN为正方形,且PM为对角线,
∴∠HPB=∠B=45°,
∴HR=![]() PB=
PB=![]() ×(14-7+t)=
×(14-7+t)=![]() ,
,
∵PM将△ABC面积平分,
∴S△PBH=![]() S△ABC,
S△ABC,
则![]() (7+t)
(7+t)![]() =
=![]() ×56,
×56,
解得t=-7+4![]() (负值舍去);
(负值舍去);
②如图5,作KT⊥AB于T,
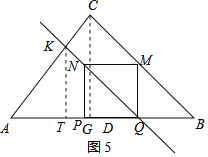
设KT=4m,由tanA=![]() 知AT=3m,
知AT=3m,
∵∠KQT=45°,
∴KT=QT=4m,
则AQ=3m+4m=7m,
又AQ=14-(7-t)=7+t,
则7m=7+t,
∴m=![]() ,
,
∵直线NQ将△ABC面积平分,
∴S△AKQ=![]() S△ABC,即
S△ABC,即![]() ×7m×4m=
×7m×4m=![]() ×56,
×56,
整理,得:m2=2,
则(![]() span>)2=2,
span>)2=2,
解得:t=-7+7![]() (负值舍去),
(负值舍去),
综上,t的值为4![]() -7或7
-7或7![]() -7.
-7.