��Ŀ����
����Ŀ�����壺����ƽ��ֱ������ϵxOy�еĵ�P��a��b����ֱ��y=ax+b�����dzƵ�P����a��b����ֱ��y=ax+b�Ĺ����㣬ֱ��y=ax+b�ǵ�P��a��b���Ĺ���ֱ�ߣ��ر�أ���a=0ʱ��ֱ��y=b��bΪ�������Ĺ�����ΪP��0��b����
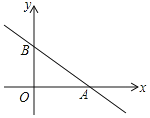
��ͼ����֪��A��-2��-2����B��4��-2����C��1��4����
��1����A�Ĺ���ֱ�ߵĽ���ʽΪ______��
ֱ��AB�Ĺ����������Ϊ______��
��2����ֱ��AC�Ĺ�����Ϊ��D��ֱ��BC�Ĺ�����Ϊ��E����P��y���ϣ���S��DEP=2�����P�����꣮
��3����M��m��n�������߶�AC��CB�������˵�A��B���ϵ�һ�����㣮ֱ��l�ǵ�M�Ĺ���ֱ�ߣ���ֱ��l����ABCǡ������������ʱ��ֱ��д��m��ȡֵ��Χ��
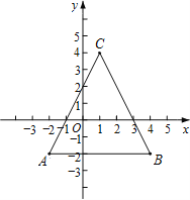
���𰸡���1��y=-2x-2����0��-2������2��P��0��5����P��0��3������3��-2��m��![]() ����2��m��4
����2��m��4
��������
��1�����ô���ϵ�������ֱ��AB�Ľ���ʽ�����ݹ��������ֱ�ߵĶ���ɵý��ۣ�
��2���ȸ��ݹ�������D��E�����꣬�����������ʽ�ɵ�P�����ꣻ
��3����M�ֱ����߶�AC��CB�����ۣ�����ֱ��l���ABCǡ������������ʱ���ɵ�m��ȡֵ��Χ��
�⣺��1����ֱ��AB�Ľ���ʽΪ��y=kx+b��
�ѵ�A��-2��-2����B��4��-2������ã�
![]() ��
��
��ã�![]() ��
��
��ֱ��AB�Ľ���ʽΪ��y=-2��
���A�Ĺ���ֱ�ߵĽ���ʽΪy=-2x-2��
ֱ��AB�Ĺ����������Ϊ����0��-2����
�ʴ�Ϊ��y=-2x-2����0��-2����
��2���ߵ�A��-2��-2����B��4��-2����C��1��4����
��ֱ��AC�Ľ���ʽΪy=2x+2��
ֱ��BC�Ľ���ʽΪy=-2x+6��
��D��2��2����E��-2��6����
��ֱ��DE�Ľ���ʽΪy=-x+4��
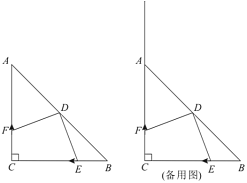
��ֱ��DE��y�ύ�ڵ�F��0��4������ͼ1��

���P��0��y����
��S��DEP=2��
��S��DEP=S��EFP+S��DFP
=![]() ��|-2|+
��|-2|+![]() =2��
=2��
��ã�y=5��y=3��
��P��0��5����P��0��3����
��3���ٵ�M���߶�AC��ʱ����ͼ3��

��AC��y=2x+2��
����M��m��2m+2����-2��m��1���������ֱ��l��y=mx+2m+2��
��C��1��4������y=mx+2m+2�ã�m+2m+2=4��m=![]() ��
��
��-2��m��![]() ��
��
�ڵ�M���߶�BC��ʱ����ͼ3��

��BC��y=-2x+6��
����M��m��-2m+6����1��m��4���������ֱ��l��y=mx-2m+6��
��A��-2��-2������y=mx-2m+6�ã�-2m-2m+6=-2��m=2��
��2��m��4��
�ۺ�������-2��m��![]() ��2��m��4��
��2��m��4��