Question

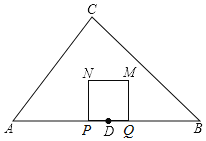
【题目】如图①所示，点将线段分成两部分，如果，那么称点为线段的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线将一个面积为的图形分成两部分，这两部分的面积分别为，，如果，那么称直线为该图形的黄金分割线．

问题探究：

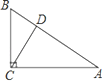
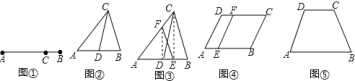
（1）研究小组猜想：在中，若点为上的黄金分割点，如图②，则直线是的黄金分割线，你认为呢？为什么？

（2）研究小组在进一步探究中发现：过点任作一条直线交于点，再过点作直线，交于点，连接如图③，则直线也是的黄金分割线，请你说明理由．

（3）如图④，点是平行四边形的边的黄金分割点，过点作，交于点，显然直线是平行四边形的黄金分割线，请你画一条平行四边形的黄金分割线，使它不经过四边形各边黄金分割点．

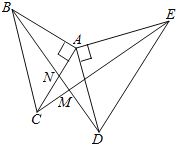
（4）如图⑤等腰梯形，请你画出它的一条黄金分割线，使它不经过各边的黄金分割点．

Answer 1

【答案】（1）直线是的黄金分割线，理由见解析；（2）直线也是的黄金分割线，理由见解析；（3）直线就是平行四边形的黄金分割线；（4）直线就是等腰梯形的黄金分割线．

【解析】

(1)若点D为AB边上的黄金分割点，则有=.如果设△ABC的边AB上的高为h，根据三角形的面积公式，易得=，=，即有=，根据图形的黄金分割线的定义即可判断；

(2)由于直线CD是△ABC的黄金分割线，所以=．要想说明直线EF也是△ABC的黄金分割线，只需证明=，即证S△ADC=S△AEF，S△BDC=S四边形BEFC即可．因为DF∥CE，所以△DFC和△DFE的公共边DF上的高也相等，所以有S△DFC=S△DFE，所以S△ADC=S△ADF+S△DFC=S△ADF+S△DFE=S△AEF，S△BDC=S四边形BEFC．

(3)根据黄金分割线的定义即可作出．本题答案不唯一，作法有无数种．

(4) 分别作出AB、CD的黄金分割点E、F，在FC上取一点N，连接EN，再过点F作FM//NE交AB于点M，连接MN即可.

解：（1）设边上的高为，

∵，，，

∴，，

∵点为上的黄金分割点，

∴，

∴，

∴直线是的黄金分割线；

（2）∵，

∴和的公共边上的高也相等，

∴，

如图③，设直线与直线交于点，

∵，

∴，

，

∵，

∴，

∴直线也是的黄金分割线；

（3）如图④，在上取一点，连接，再过点作交于点，连接，

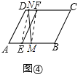
则直线就是平行四边形的黄金分割线；

（4）如图⑤，分别作出、的黄金分割点、，在上取一点，连接，再过点作交于点，连接，

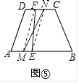
则直线就是等腰梯形的黄金分割线．

故答案为：（1）直线是的黄金分割线，理由见解析；（2）直线也是的黄金分割线，理由见解析；（3）直线就是平行四边形的黄金分割线；（4）直线就是等腰梯形的黄金分割线．