ЬтФПФкШн
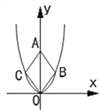
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌЕуOЮЊзјБъдЕуЃЌОиаЮOABCЕФБпOAЃЌOCдкзјБъжсЩЯЃЌЕуBЃЈ12ЃЌ4ЃЉЃЌЕуDЃЈ3ЃЌ0ЃЉЃЌЕуEЃЈ0ЃЌ2ЃЉЃЌЙ§ЕуDзїDFЁЭDEЃЌНЛABгкЕуFЃЌСЌНсEFЃЌНЋЁїDEFШЦЕуEФцЪБеыЗНЯђа§зЊЃЌа§зЊНЧЖШЮЊІШЃЈ0ЁуЃМІШЃМ180ЁуЃЉЃЎ
ЃЈ1ЃЉЧѓtanЁЯDFEЃЎ
ЃЈ2ЃЉдка§зЊЙ§ГЬжаЃЌЕБЁїDFEЕФвЛБпгыжБЯпABЦНааЪБЃЌЧѓжБЯпABНиЁїDFEЫљЕУЕФШ§НЧаЮЕФУцЛ§ЃЎ
ЃЈ3ЃЉдка§зЊЙ§ГЬжаЃЌЕБЁЯDFEЕФСНБпЫљдкжБЯпгыyжсЮЇГЩЕФШ§НЧаЮЮЊЕШбќШ§НЧаЮЪБЃЌЧѓЕуFЕФзјБъЃЎ

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉМћНтЮі.
ЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉМћНтЮі.
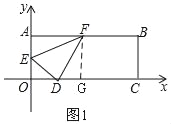
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉШчЭМ1ЃЌзїИЈжњЯпЃЌЙЙНЈЯрЫЦШ§НЧаЮЃЌИљОнЯрЫЦБШЧѓDGЕФГЄЃЌРћгУЙДЙЩЖЈРэЗжБ№ЧѓDEКЭDFЕФГЄЃЌгЩШ§НЧКЏЪ§ЖЈвхМЦЫуtanЁЯDFEЕФжЕЃЛ
ЃЈ2ЃЉЗжШ§жжЧщПіЃК
ЂйЕБEDЁЮABЪБЃЌШчЭМ2ЃЌДЫЪБжБЯпABНиЁїDFEЫљЕУЕФШ§НЧаЮЪЧЁїFGHЃЌ
ЂкЕБDFЁЮABЪБЃЌШчЭМ3ЃЌДЫЪБжБЯпABНиЁїDFEЫљЕУЕФШ§НЧаЮЪЧЁїAGEЃЌ
ЂлЕБEFЁЮABЪБЃЌШчЭМ4ЃЌДЫЪБжБЯпABНиЁїDFEЫљЕУЕФШ§НЧаЮЪЧЁїDGHЃЌ
ДњШыУцЛ§ЙЋЪНЧѓГіУцЛ§МДПЩЃЛ
ЃЈ3ЃЉЗжЫФжжЧщПіЃК
ЂйШчЭМ5ЃЌЕБGF=EF=![]() ЪБЃЌИљОнШ§НЧКЏЪ§ЕУЃКtanЁЯG=
ЪБЃЌИљОнШ§НЧКЏЪ§ЕУЃКtanЁЯG=![]() ЃЌдђ
ЃЌдђ![]() ЃЌЩшFH=aЃЌGH=3aЃЌдђGF=
ЃЌЩшFH=aЃЌGH=3aЃЌдђGF=![]() aЃЌЧѓГіaЕФжЕЃЌаДГіFЕФзјБъЃЛ
aЃЌЧѓГіaЕФжЕЃЌаДГіFЕФзјБъЃЛ
ЂкЕБGF=GEЪБЃЌШчЭМ6ЃЌзїИЈжњЯпЃЌжЄУїЁїEFHЁеЁїFEDЃЌЧѓFHКЭOHЕФГЄЃЌаДГіFЕФзјБъЃЛ
ЂлЕБFG=EF=![]() ЪБЃЌШчЭМ7ЃЌЧѓDGЕФГЄЃЌРћгУЙДЙЩЖЈРэЧѓEG=
ЪБЃЌШчЭМ7ЃЌЧѓDGЕФГЄЃЌРћгУЙДЙЩЖЈРэЧѓEG=![]() ЃЌРћгУУцЛ§ЗЈЧѓFHЕФГЄЃЌаДГіFЕФзјБъЃЛ
ЃЌРћгУУцЛ§ЗЈЧѓFHЕФГЄЃЌаДГіFЕФзјБъЃЛ
ЂмЕБEG=EF=![]() ЪБЃЌШчЭМ8ЃЌИљОнtanЁЯDFE=tanЁЯDGE=
ЪБЃЌШчЭМ8ЃЌИљОнtanЁЯDFE=tanЁЯDGE=![]() =
=![]() ЃЌЩшFH=3bЃЌGH=4bЃЌдђFG=5bЃЌ
ЃЌЩшFH=3bЃЌGH=4bЃЌдђFG=5bЃЌ
ЧѓГіbЕФжЕЃЌМЦЫуOHКЭFHЕФГЄЃЌаДГіFзјБъЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉШчЭМ1ЃЌЙ§FзїFGЁЭOCгкGЃЌдђFG=4ЃЌ
ЁпЕуDЃЈ3ЃЌ0ЃЉЃЌЕуEЃЈ0ЃЌ2ЃЉЃЌ
ЁрOE=2ЃЌOD=3ЃЌ
ЁпDFЁЭDEЃЌ
ЁрЁЯEDF=90ЁуЃЌ
ЁрЁЯEDO+ЁЯFDC=90ЁуЃЌ
ЁпЁЯEOD=90ЁуЃЌ
ЁрЁЯOED+ЁЯEDO=90ЁуЃЌ
ЁрЁЯOED=ЁЯFDCЃЌ
ЁпЁЯEOD=ЁЯFGD=90ЁуЃЌ
ЁрЁїFDGЁзЁїDEOЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрDG=![]() ЃЌ
ЃЌ
гЩЙДЙЩЖЈРэЕУЃКDF=![]() =
=![]() =
=![]() ЃЌ
ЃЌ
ED=![]() =
=![]() ЃЌ
ЃЌ
дкRtЁїDEFжаЃЌtanЁЯDFE=![]() =
=![]() =
=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЗжШ§жжЧщПіЃК
ЂйЕБEDЁЮABЪБЃЌШчЭМ2ЃЌДЫЪБжБЯпABНиЁїDFEЫљЕУЕФШ§НЧаЮЪЧЁїFGHЃЌ
ЁпDFЁЭDEЃЌ
ЁрABЁЭDFЃЌ
ЁрDH=AE=2ЃЌ
ЁрFH=DFЉDH=![]() Љ2ЃЌ
Љ2ЃЌ
гЩtanЁЯF=![]() =
=![]() ЕУЃК
ЕУЃК =
=![]() ЃЌ
ЃЌ
ЁрGH=![]() ЃЌ
ЃЌ
ЁрS=SЁїFGH=![]() GHFH=
GHFH=![]() ЁС
ЁС![]() ЃЈ
ЃЈ![]() Љ2ЃЉ=
Љ2ЃЉ=![]() Љ2
Љ2![]() ЃЛ
ЃЛ

ЂкЕБDFЁЮABЪБЃЌШчЭМ3ЃЌДЫЪБжБЯпABНиЁїDFEЫљЕУЕФШ§НЧаЮЪЧЁїAGEЃЌ
tanЁЯAEG=![]() =ЃЌ
=ЃЌ
ЁрЃЌ
ЁрAG=ЃЌ
ЁрS=SЁїAGE=AGAE=![]() ЁС
ЁС![]() ЁС2=
ЁС2=![]() ЃЛ
ЃЛ

ЂлЕБEFЁЮABЪБЃЌШчЭМ4ЃЌДЫЪБжБЯпABНиЁїDFEЫљЕУЕФШ§НЧаЮЪЧЁїDGHЃЌ
ЁрЁЯF=ЁЯDGHЃЌ
tanЁЯF=tanЁЯDGH=![]() =
=![]() ЃЌ
ЃЌ
ЩшDH=3xЃЌDG=4xЃЌдђGH=5xЃЌ
Й§DзїDMЁЭEFЃЌНЛGHгкNЃЌНЛEFгкMЃЌ
ЁрDN=![]() xЃЌN=AE=2ЃЌ
xЃЌN=AE=2ЃЌ
дкRtЁїDEFжаЃЌгЩЙДЙЩЖЈРэЕУЃКEF=![]() =
=![]() =
=![]() ЃЌ
ЃЌ
SЁїEDF=![]() DEDF=
DEDF=![]() EFDMЃЌ
EFDMЃЌ
![]() ЁС
ЁС![]() =
=![]() ЁСDMЃЌ
ЁСDMЃЌ
DM=![]() ЃЌ
ЃЌ
гЩDN+MN=DMЃЌЕУЃК![]() +2=
+2=![]() ЃЌ
ЃЌ
x=![]() ЃЌ
ЃЌ
S=SЁїDGH=![]() DHЁСDG=
DHЁСDG=![]() ЁС4xЁС3x=6x2=6ЁСЃЈ
ЁС4xЁС3x=6x2=6ЁСЃЈ![]() ЃЉ2=
ЃЉ2=![]() Љ
Љ![]() ЃЛ
ЃЛ

ЃЈ3ЃЉЗжЫФжжЧщПіЃК
ЂйШчЭМ5ЃЌЕБGF=EF=![]() ЪБЃЌ
ЪБЃЌ
Й§FзїFHЁЭyжсгкHЃЌдђGH=EHЃЌ
RtЁїGEDжаЃЌtanЁЯG=![]() =
=![]() ЃЌ
ЃЌ
ЁпED=![]() ЃЌGD=FG+DF=
ЃЌGD=FG+DF=![]() +
+![]() =3
=3![]() ЃЌ
ЃЌ
Ёр![]() =
=![]() =
=![]() ЃЌ
ЃЌ
ЩшFH=aЃЌGH=3aЃЌдђGF=![]() aЃЌ
aЃЌ
Ёр![]() a=
a=![]()
![]() ЃЌ
ЃЌ
a=![]() ЃЌ
ЃЌ
ЁрFH=![]() ЃЌ
ЃЌ
OH=OE+HE=2+3ЁС![]() =
=![]() +2=
+2=![]() ЃЌ
ЃЌ
ЁрFЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ

ЂкЕБGF=GEЪБЃЌШчЭМ6ЃЌ
Й§FзїFHЁЭyжсгкHЃЌ
ЁрЁЯDFE=ЁЯFEGЃЌ
ЁпЁЯFHE=ЁЯFDE=90ЁуЃЌEF=EFЃЌ
ЁрЁїEFHЁеЁїFEDЃЌ
ЁрFH=ED=![]() ЃЌHE=DF=
ЃЌHE=DF=![]() ЃЌ
ЃЌ
ЁрOH=EH+OE=![]() +2=
+2=![]() ЃЌ
ЃЌ
ЁрFЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ

ЂлЕБFG=EF=![]() ЪБЃЌШчЭМ7ЃЌ
ЪБЃЌШчЭМ7ЃЌ
DG=![]() =
=![]() ЃЌ
ЃЌ
RtЁїDEGжаЃЌ
EG=![]() =
=![]() =
=![]() ЃЌ
ЃЌ
Й§FзїFHЁЭyжсгкHЃЌ
ЁпFG=EFЃЌ
ЁрGH=EH=![]() ЃЌ
ЃЌ
ЁрOH=![]() +2=
+2=![]() ЃЌ
ЃЌ
SЁїEGF=![]() GEFH=
GEFH=![]() FGDEЃЌ
FGDEЃЌ
![]() FH=
FH=![]() ЁС
ЁС![]() ЃЌ
ЃЌ
![]() FH=
FH=![]() ЃЌ
ЃЌ
FH=![]() ЃЌ
ЃЌ
ЁрFЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ

ЂмЕБEG=EF=![]()
![]() ЪБЃЌШчЭМ8ЃЌ
ЪБЃЌШчЭМ8ЃЌ
ЁрЁЯDFE=ЁЯDGEЃЌ
ЁпEDЁЭGFЃЌ
ЁрDF=DG=![]()
![]() ЃЌ
ЃЌ
ЁрFG=2DF=![]() ЃЌ
ЃЌ
tanЁЯDFE=tanЁЯDGE=![]() =
=![]() ЃЌ
ЃЌ
ЩшFH=3bЃЌGH=4bЃЌдђFG=5bЃЌ
дђ5b=![]()
![]() ЃЌ
ЃЌ
b=![]()
![]() ЃЌ
ЃЌ
ЁрFH=3b=3ЁС![]()
![]() =
=![]() ЃЌGH=4b=4ЁС
ЃЌGH=4b=4ЁС![]() =
=![]() ЃЌ
ЃЌ
ЁрOH=OE+EGЉGH=OE+EFЉGH=2+![]() Љ
Љ![]()
![]() =
=![]() ЃЌ
ЃЌ
ЁрFЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ

злЩЯЫљЪіЃЌЕуFЕФзјБъЮЊ![]() Лђ
Лђ![]() ЛђЃЈЉ
ЛђЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈЉ
ЃЉЛђЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ