题目内容
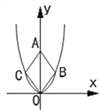
【题目】二次函数y=![]() 的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=
的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=![]() 的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为___________.
的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为___________.
【答案】2![]()
【解析】分析:连结BC交OA于D,如图,根据菱形的性质得BC⊥OA,∠OBD=60°,利用含30度的直角三角形三边的关系得OD=![]() BD,设BD=t,则OD=
BD,设BD=t,则OD=![]() t,B(t,
t,B(t,![]() t),利用二次函数图象上点的坐标特征得
t),利用二次函数图象上点的坐标特征得![]() t2=
t2=![]() t,解得t1=0(舍去),t2=1,则BD=1,OD=
t,解得t1=0(舍去),t2=1,则BD=1,OD=![]() ,然后根据菱形性质得BC=2BD=2,OA=2OD=2
,然后根据菱形性质得BC=2BD=2,OA=2OD=2![]() ,再利用菱形面积公式计算即可.
,再利用菱形面积公式计算即可.
详解:连结BC交OA于D,如图,
∵四边形OBAC为菱形,∴BC⊥OA.
∵∠OBA=120°,∴∠OBD=60°,∴OD=![]() BD,设BD=t,则OD=
BD,设BD=t,则OD=![]() t,∴B(t,
t,∴B(t,![]() t),把B(t,
t),把B(t,![]() t)代入y=
t)代入y=![]() x2得:
x2得:![]() t2=
t2=![]() t,解得:t1=0(舍去),t2=1,∴BD=1,OD=
t,解得:t1=0(舍去),t2=1,∴BD=1,OD=![]() ,∴BC=2BD=2,OA=2OD=2
,∴BC=2BD=2,OA=2OD=2![]() ,∴菱形OBAC的面积=
,∴菱形OBAC的面积=![]() ×2×2
×2×2![]() =2
=2![]() .
.
故答案为:2![]() .
.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】下表记录的是今年长江某一周的水位变化情况,这一周的上周末的水位已达到警戒水位33米(正号表示水位比前一天上升,负号表示水位比前一天下降).
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
水位变化(米) |
|
|
|
|
|
|
(1)本周哪一天长江的水位最高?位于警戒水位之上还是之下?
(2)与上周周末相比,本周周末长江的水位是上升了还是下降了?并通过计算说明理由.
【题目】观察下表三行数的规律,回答下列问题:
第1列 | 第2列 | 第3列 | 第4列 | 第5列 | 第6列 | … | |
第1行 | -2 | 4 | -8 | a | -32 | 64 | … |
第2行 | 0 | 6 | -6 | 18 | -30 | 66 | … |
第3行 | -1 | 2 | -4 | 8 | -16 | b | … |
(1)第1行的第四个数a是 ;第3行的第六个数b是 ;
(2)若第1行的某一列的数为c,则第2行与它同一列的数为 ;
(3)已知第n列的三个数的和为2562,若设第1行第n列的数为x,试求x的值.
【题目】某校举办“红歌伴我成长”歌咏比赛活动,参赛同学的成绩分别绘制成频数分布表和频数分布直方图(均不完整)如图:
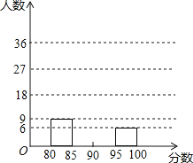
分数段 | 频数 | 频率 |
80≤x<85 | 9 | 0.15 |
85≤x<90 | m | 0.45 |
90≤x<95 | ■ | ■ |
95≤x<100 | 6 | n |
(1)求m,n的值分别是多少;
(2)请在图中补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段?