题目内容
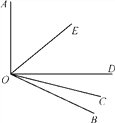
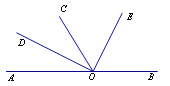
【题目】如图,OC在∠BOD内.
(1)如果∠AOC和∠BOD都是直角.
①若∠BOC=60°,则∠AOD的度数是 ;
②猜想∠BOC与∠AOD的数量关系,并说明理由;
(2)如果∠AOC=∠BOD=x°,∠AOD=y°,求∠BOC的度数.

【答案】(1)①∠AOD=120°;②猜想∠BOC+∠AOD=180°,证明见解析;(2)120°.
【解析】试题分析:(1)①根据直角的定义先求出∠AOB,再根据角的和差关系即可得出答案;
②得到∠AOD+∠BOC=∠BOD+∠AOC,代入求出即可;
(2)类比②可得:∠AOD+∠BOC=∠BOD+∠AOC,依此代入计算即可求解.
试题解析:
(1)①∵∠AOC和∠BOD都是直角,∠BOC=60°,
∴∠AOB=30°,
∴∠AOD=120°;
②猜想∠BOC+∠AOD=180°.
证明:∵∠BOC=90°,
∴∠AOD=∠BOD+∠AOB=90°+∠AOB,
∵∠AOC=90°,
∴∠AOD+∠BOC=∠BOD+∠AOC=90°+90°=180°;
(2)类比②可得:∠AOD+∠BOC=∠BOD+∠AOC,
∵∠BOD=∠AOC=x°,∠AOD=y°,
∴∠BOC=(2x﹣y)°.
故答案为:120°.

练习册系列答案
相关题目