题目内容
【题目】已知:如图,△ABC中,BD=DC,∠ABD=∠ACD,求证:AD平分∠BAC.

【答案】证明见解析.
【解析】试题分析:由BD=DC,易知∠3=∠4,再结合∠1=∠2,利用等量相加和相等可得∠ABC=∠ACB,从而可知△ABC是等腰三角形,于是AB=AC,再结合BD=DC,∠1=∠2,利用SAS可证△ABD≌△ACD,从而有∠BAD=∠CAD,即AD平分∠BAC.
试题解析:证明:如图所示,
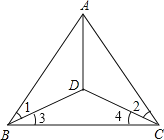
∵BD=DC,
∴∠3=∠4,
又∵∠1=∠2,
∴∠1+∠3=∠2+∠4,
即∠ABC=∠ACB,
∴△ABC是等腰三角形,
∴AB=AC,
在△ABD和△ACD中,
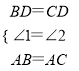
∴△ABD≌△ACD(SAS),
∴∠BAD=∠CAD,
∴AD平分∠BAC.

练习册系列答案
相关题目