题目内容
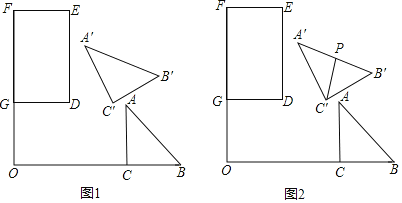
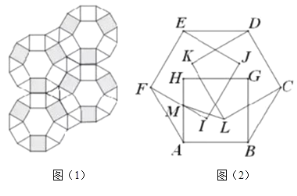
【题目】建筑工人用边长相等的正六边形、正方形、正三角形三种瓷砖铺设地面，正方形瓷砖分黑白两种颜色，密铺成图（1）的形状．用水泥浇筑前，为方便施工，工人要先把瓷砖按图1方式先摆放好，一工人摆放时，无意间将3块黑色正方形瓷砖上翻到一个正六边形的上面，其中三个正方形的一条边分别和正六边形的三条边重合，如图（2）所示．按图（2）方式给各点作上标注，若正方形的边长
，则
_____
(不考虑瓷砖的厚度)
【答案】
【解析】
过点I作
，分别交AH于点P，交BG于点Q，由正六边形和正方形性质计算
的度数，在
中，表示MP，PI，得LQ，PL的长度，
中使用勾股定理计算即可．
过点I作，分别交AH于点P，交BG于点Q
根据正六边形的每个内角为：
，即
又∵
，∴
同理可得：
∴
，
∴
是顶角为120°的等腰三角形
∵AF=AB=12
∴FM =AM=
∴MI=
在中，
，
由正六边形及正方形性质可知：
∴
在中，
故答案为：．
练习册系列答案
中考解读考点精练系列答案
相关题目
