题目内容
【题目】一个不透明的袋子里装有4个小球,分别标有1,2,3,7四个数字,这些小球除所标数字不同外,其余方面完全相同,甲、乙两人每次同时从袋子中各随机摸出一个小球,记下小球上的数字,并计算它们的和.
(1)请用画树状图或列表的方法,求两数和是8的概率;
(2)甲、乙两人想用这种方法做游戏,他们规定:若两数之和是2的倍数时,甲得3分;若两数之和是3的倍数时,乙得2分;当两数之和是其他数值时,两人均不得分.你认为这个游戏公平吗?请说明理由;若你认为不公平,请你修改得分规则,使游戏公平。
【答案】(1)画树形图见解析,两数和是8的概率![]() ;
;
(2)游戏不公平,理由见解析;将得分规则修改为:当两数和是2的倍数时,甲得2分,当两数和是3的倍数时,乙得3分,当两数之和是其他数值时,两人均不得分。
【解析】分析:(1)根据题意画树状图或列表,然后根据树状图或表格求得所有等可能的结果与两数和是8的情况,利用概率公式即可求得答案;(2)首先求得两数之和是2的倍数与两数之和是3的倍数的概率,然后比较得分,得分相同,则公平,否则不公平.
本题解析:
(1)画树形图,
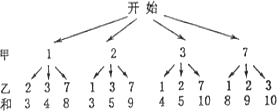
两数和是8的概率 ![]()
(2)∵两数之和是2的倍数的有6种情况,两数之和是3的倍数的有4种情况,
∴P(两数之和是2的倍数)= ![]() =
=![]() ,P(两数之和是3的倍数)=
,P(两数之和是3的倍数)= ![]() =
=![]() ,
,
∵![]() ×3≠
×3≠![]() ×2,∴游戏不公平。
×2,∴游戏不公平。
应该为:当两数之和是2的倍数时,甲得2分,当两数之和是3的倍数时,乙得3分,当两数之和是其它数值时,两人均不得分。

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目