题目内容
3. 如图,在锐角△ABC中,以AB、AC为边分别向形外作等边△ABD、△ACE,连BE和CD交于O点,BE交AC于M点,CD交AB于N点,以下结论:①BE=CD;②∠COB=120°;③OM=ON.恒成立的有①②(填上正确结论的序号).
如图,在锐角△ABC中,以AB、AC为边分别向形外作等边△ABD、△ACE,连BE和CD交于O点,BE交AC于M点,CD交AB于N点,以下结论:①BE=CD;②∠COB=120°;③OM=ON.恒成立的有①②(填上正确结论的序号).
分析 ①根据SAS即可证明△ADC≌△ABE,推出BE=DC.
②利用“8字型”证明∠DGB=∠DAB即可.
③不一定成立.
解答 解:①正确.理由:∵△ABD和△ACE都是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠CAE=60°,
∴∠DAC=∠BAE,
在△ADC和△ABE中,
$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AC=AE}\end{array}\right.$,
∴△ADC≌△ABE,
∴BE=CD.
②正确.理由:∵△ADC≌△ABE,
∴∠ADC=∠ABE,
∵∠ADC+∠AND+∠DAB=180°和∠ABE+∠BNO+∠NOB=180°、∠AND=∠BNO,
∴∠NOB=∠DAB=60°,
∴∠BOC=120°.
③错误.OM与ON不一定相等.
故答案为①②.
点评 本题考查全等三角形的判定和性质、等边三角形的性质等知识,解题的关键是正确寻找全等三角形,学会利用“8字型”证明角相等,属于中考常考题型.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
8.下列说法正确的是( )
| A. | 近似数5.05是精确到0.01的数 | |
| B. | 近似数55.0与55表示的意义是一样的 | |
| C. | 近似数5.05是精确到十分位的数 | |
| D. | 近似数5.05万精确到万位 |
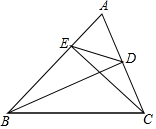 如图,在△ABC中,BD⊥AC,CE⊥AB,垂足分别为D、E,连接DE,试判断△ADE与△ABC是否相似,并说明理由?
如图,在△ABC中,BD⊥AC,CE⊥AB,垂足分别为D、E,连接DE,试判断△ADE与△ABC是否相似,并说明理由? 如图,一电线杆AB的高为10米,当太阳光线与地面的夹角为60°时,其影长AC为$\frac{10\sqrt{3}}{3}$米.
如图,一电线杆AB的高为10米,当太阳光线与地面的夹角为60°时,其影长AC为$\frac{10\sqrt{3}}{3}$米.