题目内容
14.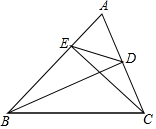 如图,在△ABC中,BD⊥AC,CE⊥AB,垂足分别为D、E,连接DE,试判断△ADE与△ABC是否相似,并说明理由?
如图,在△ABC中,BD⊥AC,CE⊥AB,垂足分别为D、E,连接DE,试判断△ADE与△ABC是否相似,并说明理由?
分析 由在△ABC中,BD,CE分别是AC,AB边上的高,易证得△ACE∽△ABD,即可得 $\frac{AE}{AD}$=$\frac{AC}{AB}$,由此可证得△ADE∽△ABC.
解答 解:相似.理由如下:
∵在△ABC中,BD,CE分别是AC,AB边上的高,
∴∠AEC=∠ADB=90°,
∵∠A=∠A,
∴△ACE∽△ABD,
∴$\frac{AE}{AD}$=$\frac{AC}{AB}$,
即 $\frac{AE}{AC}$=$\frac{AD}{AB}$,
∵∠A是公共角,
∴△ADE∽△ABC.
点评 此题考查了相似三角形的判定与性质,解题的关键是灵活运用相似三角形的判定和性质,熟练掌握相似三角形的判定,属于基础题,中考常考题型.

练习册系列答案
相关题目
5.y关于x的一次函数y=(m2+1)x+2图象上有两个点(x1,y1)和(x2,y2),若y2>y1,则( )
| A. | x1>x2 | B. | x1=x2 | C. | x1<x2 | D. | 无法判定 |
4.下列剪纸作品中是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在锐角△ABC中,以AB、AC为边分别向形外作等边△ABD、△ACE,连BE和CD交于O点,BE交AC于M点,CD交AB于N点,以下结论:①BE=CD;②∠COB=120°;③OM=ON.恒成立的有①②(填上正确结论的序号).
如图,在锐角△ABC中,以AB、AC为边分别向形外作等边△ABD、△ACE,连BE和CD交于O点,BE交AC于M点,CD交AB于N点,以下结论:①BE=CD;②∠COB=120°;③OM=ON.恒成立的有①②(填上正确结论的序号).