题目内容
【题目】(问题情境)
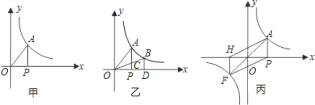
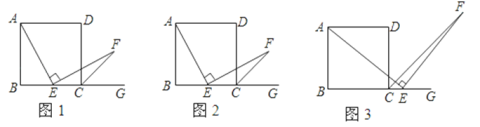
如图,在正方形ABCD中,点E是线段BG上的动点,AE⊥EF,EF交正方形外角∠DCG的平分线CF于点F.
(探究展示)
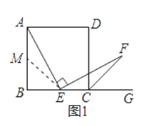
(1)如图1,若点E是BC的中点,证明:∠BAE+∠EFC=∠DCF.
(2)如图2,若点E是BC的上的任意一点(B、C除外),∠BAE+∠EFC=∠DCF是否仍然成立?若成立,请予以证明;若不成立,请说明理由.
(拓展延伸)
(3)如图3,若点E是BC延长线(C除外)上的任意一点,求证:AE=EF.
【答案】(1)证明见解析;(2)成立;证明见解析;(3)证明见解析.
【解析】
(1)取AB的中点M,连结EM,根据正方形的性质和全等三角形的判定证明即可;
(2)在AB上取一点M,使AM=CE,连接ME,根据已知条件利用ASA判定![]() ,利用全等三角形的性质证明即可.
,利用全等三角形的性质证明即可.
(3)在BA的延长线上取一点M,使AM=CE,连接ME,根据已知利用ASA判定![]() ,利用全等三角形的性质证明即可.
,利用全等三角形的性质证明即可.
(1)证明:取AB的中点M,连结EM,如图1:
∵M是AB的中点,E是BC的中点,
∴在正方形ABCD中,AM=EC,
∵CF是∠DCG的平分线,
∴∠BCF=135°,
∴∠AME=∠ECF=135°,
∵∠MAE=∠CEF=45°,
在△AME与△ECF中,
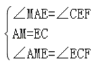 ,
,
∴△AME≌△ECF(SAS),
∴∠BAE+∠EFC=∠FCG=∠DCF;
(2)证明:取AB上的任意一点使得AM=EC,连结EM,如图2:
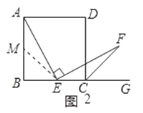
∵AE⊥EF,AB⊥BC,
∴∠BAE+∠BEA=90°,∠BEA+∠CEF=90°,
∴∠MAE=∠CEF,
∵AM=EC,
∴在正方形ABCD中,BM=BE,
∴∠AME=∠ECF=135°,
在△AME与△ECF中,
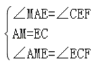 ,
,
∴△AME≌△ECF(SAS),
∴∠BAE+∠EFC=∠FCG=∠DCF;
(3)证明:取AB延长线上的一点M使得AM=CE,如图3:
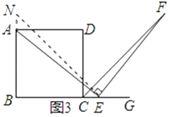
∵AM=CE,AB⊥BC,
∴∠AME=45°,
∴∠ECF=AME=45°,
∵AD∥BE,
∴∠DAE=∠BEA,
∵MA⊥AD,AE⊥EF,
∴∠MAE=∠CEF,
在△AME与△ECF中,
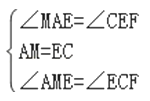 ,
,
∴△AME≌△ECF(SAS),
∴AE=EF.

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案