题目内容
【题目】函数![]() 和
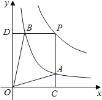
和![]() 在第一象限内的图象如图所示,点
在第一象限内的图象如图所示,点![]() 是
是![]() 的图象上一动点,作
的图象上一动点,作![]() 轴于点
轴于点![]() ,交
,交![]() 的图象于点
的图象于点![]() ,作
,作![]() 轴于点
轴于点![]() ,交
,交![]() 的图象于点
的图象于点![]() ,给出如下结论:①
,给出如下结论:①![]() 与
与![]() 的面积相等;②
的面积相等;②![]() 与
与![]() 始终相等;③四边形
始终相等;③四边形![]() 的面积大小不会发生变化;④
的面积大小不会发生变化;④![]() ,其中正确的结论序号是( )
,其中正确的结论序号是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②④
【答案】C
【解析】
设点P的坐标为(m,![]() )(m>0),则A(m,
)(m>0),则A(m,![]() ),C(m,0),B(
),C(m,0),B(![]() ,
,![]() )D(0,
)D(0,![]() ).①根据反比例函数系数k的几何意义即可得出S△ODB=S△OCA,该结论正确;②由点的坐标可找出PA=
).①根据反比例函数系数k的几何意义即可得出S△ODB=S△OCA,该结论正确;②由点的坐标可找出PA=![]() ,PB=
,PB=![]() ,由此可得出只有m=2是PA=PB,该结论不成;③利用分割图形法求图形面积结合反比例系数k的几何意义即可得知该结论成立;④结合点的坐标即可找出PA=
,由此可得出只有m=2是PA=PB,该结论不成;③利用分割图形法求图形面积结合反比例系数k的几何意义即可得知该结论成立;④结合点的坐标即可找出PA=![]() ,AC=
,AC=![]() ,由此可得出该结论成立.综上即可得出正确的结论为①③④.
,由此可得出该结论成立.综上即可得出正确的结论为①③④.
解:设点P的坐标为(m,![]() )(m>0),则A(m,
)(m>0),则A(m,![]() ),C(m,0),B(
),C(m,0),B(![]() ,
,![]() ),D(0,
),D(0,![]() ).
).
①S△ODB=![]() ×1=
×1=![]() ,S△OCA=
,S△OCA=![]() ×1=
×1=![]() ,
,
∴△ODB与△OCA的面积相等,①成立;
②PA=![]() -
-![]() =
=![]() ,PB=m-
,PB=m-![]() =
=![]() ,
,
令PA=PB,即![]() =
=![]() ,
,
解得:m=2.
∴当m=2时,PA=PB,②不正确;
③S四边形PAOB=S矩形OCPD-S△ODB-S△OCA=4-![]() -
-![]() =3.
=3.
∴四边形PAOB的面积大小不会发生变化,③正确;
④∵PA=![]() -
-![]() =
=![]() ,AC=
,AC=![]() -0=
-0=![]() ,
,
∵![]() =3×
=3×![]() ,
,
∴PA=3AC,④正确.
综上可知:正确的结论有①③④.
故选:C.

练习册系列答案
相关题目