题目内容
【题目】在平面直角坐标系中,A(5,0),B(0,5).
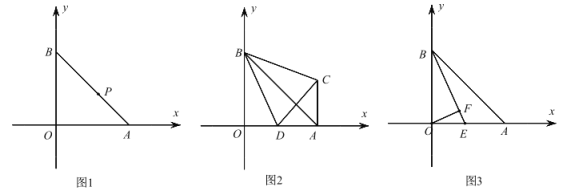
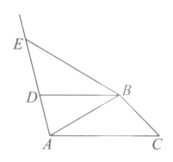
(1)如图 1,P 是 AB 上一点且![]()
![]() ,求 P 点坐标;
,求 P 点坐标;
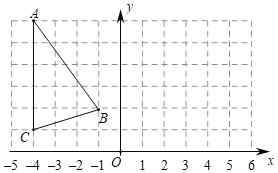
(2)如图 2,D 为 OA 上一点,AC∥OB 且∠CBO=∠DCB,求∠CBD 的度数;
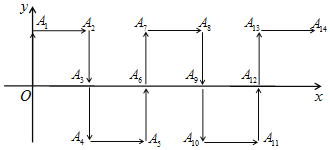
(3)如图 3,E 为 OA 上一点,OF⊥BE 于 F,若∠BEO=45°+∠EOF,求![]() 的值
的值
【答案】(1)(3,2) (2)45° (3)2
【解析】
(1)作PG⊥x轴于G,PN⊥y轴于N,根据相似三角形的性质列出比例式,分别求出PG,PN,得到P点坐标;
(2)作BG⊥AC交AC的延长线于G,作BH⊥CD于H,分别证明△BCH≌△BCG和Rt△BOD≌Rt△BHD,根据全等三角形的性质得到∠CBH=∠CBG,∠BOD=∠HOD,结合图形计算;
(3)根据题意和三角形内角和定理分别求出∠BEO=67.5°,∠EOF=22.5°,作∠BOP=∠OBE,设OF=a,根据三角形外角的性质,相似三角形的性质分别求出BF,EF,代入计算即可.
(1)作PG⊥x轴于G,PN⊥y轴于N,
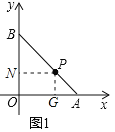
∵![]()
![]()
∴![]()
∵A(5,0),B(0,5),
∴OA=5,OB=5,
∵PG⊥x轴,
∴PG∥OB,
∴△AGP∽△AOB,
∴![]() ,即
,即![]() ,
,
解得,PG=2,
同理,PN=3,
∴P点坐标为(3,2);
(2)作BG⊥AC交AC的延长线于G,作BH⊥CD于H,
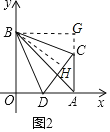
∴四边形BOAG为矩形,
∴BO=BG,
∵OA=OB,
∴矩形BOAG为正方形,
∵AC∥OB
∴∠CBO=∠BCG,
∵∠CBO=∠DCB,
∴∠BCG=∠DCB,
在△BCH和△BCG中,
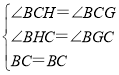 ,
,
∴△BCH≌△BCG(AAS),
∴∠CBH=∠CBG,BG=BH,
∴BO=BH,
在Rt△BOD和Rt△BHD中,
![]()
∴Rt△BOD≌Rt△BHD(HL),
∴∠BOD=∠HOD,
∴∠CBD=∠DBH+∠CBH=![]() ∠OBG=45°;
∠OBG=45°;
(3)
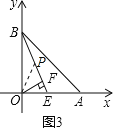
∵∠BEO=45°+∠EOF,∠BEO+∠EOF=90°,
∴∠BEO=67.5°,∠EOF=22.5°,
则∠OBE=22.5°,
作∠BOP=∠OBE=22.5°,
则PB=PO,∠OPF=45°,
设OF=a,则PF=OF=a,
由勾股定理得,OP=![]() a,
a,
∴PB=![]() a,
a,
∴BF=![]() a+a,
a+a,
∵∠BOP=∠OBE,∠OFB=∠EFO=90°,
∴△OFB∽△EFO,
∴EF=![]() a-a,
a-a,
∴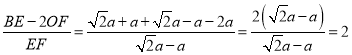

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案