题目内容
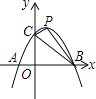
【题目】如图,在平面直角坐标系xOy中,O为坐标原点,点A(a,0),B(m,n),C(p,n),其中m>p>0,n>0,点A,C在直线y=﹣2x+10上,AC=2![]() ,OB平分∠AOC.
,OB平分∠AOC.
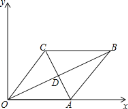
(1)求△OAC的面积;
(2)求证:四边形OABC是菱形;
(3)射线OB上是否存在点P,使得△PAC为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)S△AOC=10;(2)见解析;(3)存在,理由见解析.P(2,1)或(6,3).
【解析】
(1)先根据点A(a,0)在直线y=-2x+10上,求得点A的坐标,在Rt△ACE中,根据勾股定理列出方程(5-p)2+n2=(2![]() )2,再根据点C(p,n)在直线y=-2x+10上,得到方程n=-2p+10,进而求得n和p的值,根据点C的坐标,即可得出结论;
)2,再根据点C(p,n)在直线y=-2x+10上,得到方程n=-2p+10,进而求得n和p的值,根据点C的坐标,即可得出结论;
(2)求得OC的长,最后根据菱形的定义判定四边形OABC是菱形;
(3)先判断出∠APC=90°,再求出直线OB的解析式,利用等腰直角三角形的性质建立方程即可得出结论.
(1)∵点A(a,0)在直线y=﹣2x+10上,
∴0=﹣2a+10,即a=5,
∴A(5,0),即OA=5,
过C作CE⊥OA于点E,
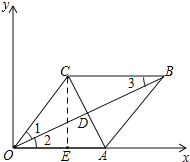
则∠AEC=90°,AE=5﹣p,
∵在Rt△ACE中,AE2+CE2=AC2,
∴(5﹣p)2+n2=(2![]() )2,
)2,
又∵点C(p,n)在直线y=﹣2x+10上,
∴n=﹣2p+10,
∴(5﹣p)2+(﹣2p+10)2=(2![]() )2,
)2,
解得p1=3,p2=7,
∴当p=3时,n=4;当p=7时,n=﹣4(舍去),
∴C(3,4),∴S△AOC=![]() OA×|yC|=
OA×|yC|=![]() ×5×4=10;
×5×4=10;
(2)在Rt△OCE中,OC=![]() =5,
=5,
∴OC=OA,
∵OB平分∠AOC,
∴∠1=∠2,
∵B(m,n),C(p,n),
∴BC∥x轴,
∴∠3=∠2,
∴∠1=∠3,
∴OC=BC=5,
∴OA∥BC,且OA=BC,
∴四边形OABC是平行四边形,
∵OC=OA,
∴平行四边形OABC是菱形;
(3)存在,理由:
如图1,
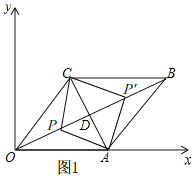
∵四边形OABC是菱形,
∴AD=CD,AC⊥OB,
∵A(5,0),C(3,4),
∴D(4,2),B(8,4),
设直线OB的解析式为y=kx,
∴8k=4,
∴k=![]() ,
,
∴直线OB的解析式为y=![]() x,
x,
设P(m,![]() m),
m),
∴DP=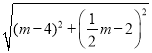 =
=![]() |m﹣4|,
|m﹣4|,
∵△PAC为直角三角形,
∴∠APC=90°,
∴DP=AD=CD=![]() AC,
AC,
∴![]() |m﹣4|=
|m﹣4|=![]() ,
,
∴m=2或m=6,
∴P(2,1)或(6,3).