题目内容
【题目】二次函数![]() ,当
,当![]() 且
且![]() 时,
时,![]() 的最小值为
的最小值为![]() ,最大值为
,最大值为![]() ,则
,则![]() 的值为( )
的值为( )
A. 2B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
二次函数![]() 的开口向下,对称轴为x=2,当x<2时,y随x的增大而增大,当x>2时,y随x的增大而减小,因为m≤x≤n且mn<0,可知m<0,n>0,需要分两种情况:①m≤0≤x≤n<2,②m≤0≤x≤2≤n讨论函数的最值情况;对于①,当x=m时y取最小值,当x=n时y取最大值,对于②,当x=m或n时y取最小值,当x=2时y取最大值,由此求出m、n的值,注意检验是否符合取值范围.
的开口向下,对称轴为x=2,当x<2时,y随x的增大而增大,当x>2时,y随x的增大而减小,因为m≤x≤n且mn<0,可知m<0,n>0,需要分两种情况:①m≤0≤x≤n<2,②m≤0≤x≤2≤n讨论函数的最值情况;对于①,当x=m时y取最小值,当x=n时y取最大值,对于②,当x=m或n时y取最小值,当x=2时y取最大值,由此求出m、n的值,注意检验是否符合取值范围.
二次函数![]() 的大致图象如下
的大致图象如下
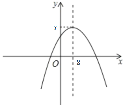
①当![]() 时,当x=m时y取最小值,即
时,当x=m时y取最小值,即![]() ,
,
解得m=3(舍去)或者m=-1,
当x=n时y取最大值,即![]() ,
,
解得n=3或者n=-1(均不符合题意,舍去);
②当![]() 时,当x=m时y取最小值,即
时,当x=m时y取最小值,即![]() ,
,
解得m=3(舍去)或者m=-1,
当x=2时,y取得最大值7,即2n=7,解得n=![]() ,
,
所以![]() .
.
故选B.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
【题目】2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |

(1)求y1与x之间的函数关系式.
(2)求y2与x之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所第获得的利润最大?最大利润是多少元?