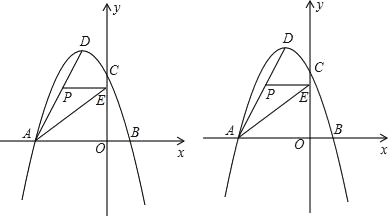题目内容
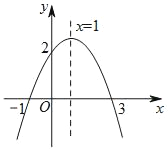
【题目】二次函数y=ax2+bx+c(a≠0,a,b,c为常数)图象如图所示,根据图象解答问题.
(1)写出过程ax2+bx+c=0的两个根.
(2)写出不等式ax2+bx+c>0的解集.
(3)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
【答案】(1)x1=﹣1,x2=3;(2)﹣1<x<3;(3)k的范围为k<![]() .
.
【解析】
(1)根据图象可知x=-1和3是方程的两根;
(2)找出函数值大于0时x的取值范围即可;;
(3)若方程ax2+bx+c=k有两个不相等的实数根,则k必须小于y=ax2+bx+c(a≠0)的最大值,据此求出k的取值范围.
(1)由图象得:ax2+bx+c=0的两个根为x1=﹣1,x2=3;
(2)由图象得:不等式ax2+bx+c>0的解集为﹣1<x<3;
(3)设抛物线解析式为y=a(x+1)(x﹣3),
把(0,2)代入得:﹣3a=2,
解得:a=﹣![]() ,
,
∴抛物线解析式为y=﹣![]() (x+1)(x﹣3)=﹣
(x+1)(x﹣3)=﹣![]() x2+
x2+![]() x+2=﹣
x+2=﹣![]() (x﹣1)2+
(x﹣1)2+![]() ,
,
∵方程ax2+bx+c=k有两个不相等的实数根
∴二次函数与y=k有两个交点,
由图象得:k的范围为k<![]() .
.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目