题目内容
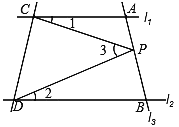
【题目】如图,四边形ABCD中AC平分∠BAD,∠ADC=∠ACB=90![]() ,E为AB的中点,AC与DE交于点F.
,E为AB的中点,AC与DE交于点F.

(1)求证: ![]() =AB·AD;
=AB·AD;
(2)求证:CE//AD;
(3)若AD=6, AB=8.求 ![]() 的值.
的值.
【答案】(1)证明见解析; (2)证明见解析; (3) ![]() .
.
【解析】试题分析:(1)由AC平分∠BAD,∠ADC=∠ACB=90°,可证得△ADC∽△ACB,然后由相似三角形的对应边成比例,证得AC2=ABAD;
(2)由E为AB的中点,根据在直角三角形中,斜边上的中线等于斜边的一半,即可证得CE=![]() AB=AE,继而可证得∠DAC=∠ECA,得到CE∥AD;
AB=AE,继而可证得∠DAC=∠ECA,得到CE∥AD;
(3)易证得△AFD∽△CFE,然后由相似三角形的对应边成比例,求得![]() 的值.
的值.
试题解析:(1)证明:∵AC平分∠BAD,∴∠DAC=∠CAB,∵∠ADC=∠ACB=90°,∴△ADC∽△ACB,∴AD:AC=AC:AB,∴AC2=ABAD;
(2)证明:∵E为AB的中点,∴CE=![]() AB=AE,∴∠EAC=∠ECA,∵∠DAC=∠CAB,∴∠DAC=∠ECA,∴CE∥AD;
AB=AE,∴∠EAC=∠ECA,∵∠DAC=∠CAB,∴∠DAC=∠ECA,∴CE∥AD;
(3)解:∵CE∥AD,∴△AFD∽△CFE,∴AD:CE=AF:CF,∵CE=![]() AB,∴CE=
AB,∴CE=![]() ×8=4,∵AD=6,∴6:4=AF:CF,∴
×8=4,∵AD=6,∴6:4=AF:CF,∴![]() =
=![]() =
=![]() .
.

练习册系列答案
相关题目
【题目】已知函数![]() ,画出图象并根据函数图象回答下列问题:
,画出图象并根据函数图象回答下列问题:
(1)列表、描点、连线
x | |||||
|
(2)![]() 的两个解是多少?
的两个解是多少?
(3)x取何值时,y>0?
(4)x取何值时,抛物线在x轴上或下方?
(5)抛物线![]() 与直线y=k有唯一的交点,则k= .
与直线y=k有唯一的交点,则k= .