题目内容
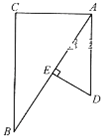
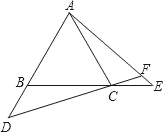
【题目】如图:已知在等边三角形ABC中,点D、E分别是AB、BC延长线上的点,且BD=CE,直线CD与AE相交于点F.
(1)求证:DC=AE;
(2)求证:AD2=DCDF.
【答案】(1)证明见解析(2)证明见解析
【解析】
(1)利用“SAS”证明△DBC≌△ECA即可;
(2)由△DBC≌△ECA可知∠E=∠D,根据外角定理可知∠AFC=∠E+∠FCE=∠D+∠BCD=∠ABC=60°,可证△DCA∽△DAF,利用相似比得出结论.
(1)∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠BAC=60°,BC=CA
∴∠DBC=∠ECA=180°﹣60°=120°
在△DBC与△ECA中
∴△DBC≌△ECA(SAS)
∴DC=AE;
(2)∵△DBC≌△ECA,
∴∠DCB=∠EAC
又∠ACB=∠BAC
∴∠DCA=∠DAF
又∠D=∠D
∴△DCA∽△DAF
∴![]()
∴AD2=DCDF.

练习册系列答案
相关题目