题目内容
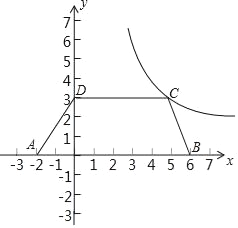
【题目】如图,在四边形ABCD中,CD∥AB,AD=BC.已知A(﹣2,0),B(6,0),D(0,3),函数y=![]() (x>0)的图象G经过点C.
(x>0)的图象G经过点C.
(1)求点C的坐标和函数y=![]() (x>0)的表达式;
(x>0)的表达式;
(2)将四边形ABCD向上平移2个单位得到四边形A'B'C'D',问点B'是否落在图象G上?
【答案】(1)C(4,3),反比例函数的解析式y=![]() ;(2)点B′恰好落在双曲线上.
;(2)点B′恰好落在双曲线上.
【解析】
(1)过C作CE⊥AB,由题意得到四边形ABCD为等腰梯形,进而得到三角形AOD与三角形BEC全等,得到CE=OD=3,OA=BE=2,由AB﹣AO﹣BE求出OE的长,确定出C坐标,代入反比例解析式求出k的值即可;
(2)由平移规律确定出B′的坐标,代入反比例解析式检验即可.
(1)过C作CE⊥AB.
∵DC∥AB,AD=BC,∴四边形ABCD为等腰梯形,∴∠A=∠B,DO=CE=3,CD=OE,∴△ADO≌△BCE,∴BE=OA=2.
∵AB=8,∴OE=AB﹣OA﹣BE=8﹣2﹣2=4,∴C(4,3),把C(4,3)代入反比例解析式得:k=12,则反比例解析式为y![]() ;
;
(2)由平移得:平移后B的坐标为![]() (6,2),把x=6代入反比例得:y=2,则平移后点
(6,2),把x=6代入反比例得:y=2,则平移后点![]() 落在该双曲线上.
落在该双曲线上.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目