题目内容
【题目】如图,![]() 为
为![]() 的内接三角形,
的内接三角形,![]() 为
为![]() 的直径,过点
的直径,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() ;
;
(2)过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)若点![]() 为直径
为直径![]() 下方半圆的中点,连接
下方半圆的中点,连接![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的长.
的长.
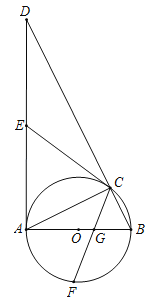
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)利用AB是圆O的直径和AD是圆O的切线判断出∠ACD=∠DAB=90°,即可得出结论;
(2)利用切线长定理判断出AE=CE,从而得到∠DAC=∠EAC,再用等角的余角相等判断出∠D=∠DCE,得出DE=CE,即可得到结论;
(3)先求出tan∠ABD的值,进而得出GH=2CH,进而得到BC=3BH,再求出BC建立方程求BH,从而求出GH.
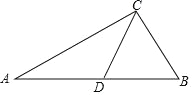
(1)∵AB是⊙O直径,∴∠ACD=∠ACB=90°.
∵AD是⊙O的切线,∴∠BAD=90°,∴∠ACD=∠DAB=90°.
∵∠D=∠D,∴△DAC∽△DBA;
(2)∵EA,EC是⊙O的切线,∴AE=CE(切线长定理),∴∠DAC=∠ECA.
∵∠ACD=90°,∴∠ACE+∠DCE=90°,∠DAC+∠D=90°,∴∠D=∠DCE,∴DE=CE,∴AD=AE+DE=CE+CE=2CE,∴CE![]() AD;
AD;
(3)如图,在Rt△ABD中,AD=6,AB=3,∴tan∠ABD![]() 2,过点G作GH⊥BD于H,∴tan∠ABD
2,过点G作GH⊥BD于H,∴tan∠ABD![]() 2,∴GH=2BH.
2,∴GH=2BH.
∵点F是直径AB下方半圆的中点,∴∠BCF=45°,∴∠CGH=∠CHG﹣∠BCF=45°,∴CH=GH=2BH,∴BC=BH+CH=3BH.在Rt△ABC中,tan∠ABC![]() 2,∴AC=2BC,根据勾股定理得:AC2+BC2=AB2,∴4BC2+BC2=9,∴BC
2,∴AC=2BC,根据勾股定理得:AC2+BC2=AB2,∴4BC2+BC2=9,∴BC![]() ,∴3BH
,∴3BH![]() ,∴BH
,∴BH![]() ,∴GH=2BH
,∴GH=2BH![]() .在Rt△CHG中,∠BCF=45°,∴CG
.在Rt△CHG中,∠BCF=45°,∴CG![]() GH
GH![]() .
.

练习册系列答案
相关题目