题目内容
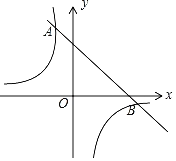
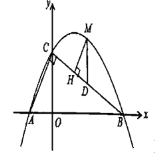
【题目】如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 在
在![]() 轴上,
轴上,![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点.
两点.
(1)求![]() 两点的坐标;
两点的坐标;
(2)求抛物线的解析式;
(3)点![]() 是直线
是直线![]() 上方抛物线上的一点,过点
上方抛物线上的一点,过点![]() 作
作![]() 于点
于点![]() ,作
,作![]() 轴交
轴交![]() 于点
于点![]() ,求
,求![]() 周长的最大值.
周长的最大值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由直线解析式可求得B、C坐标,在Rt△BOC中由三角函数定义可求得∠OCB=60°,则在Rt△AOC中可得∠ACO=30°,利用三角函数的定义可求得OA,则可求得A点坐标;
(2)由A、B两点坐标,利用待定系数法可求得抛物线解析式;
(3)由平行线的性质可知∠MDH=∠BCO=60°,在Rt△DMH中利用三角函数的定义可得到DH、MH与DM的关系,可设出M点的坐标,则可表示出DM的长,从而可表示出△DMH的周长,利用二次函数的性质可求得其最大值.
解:(1)![]() 直线
直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于
轴交于![]() 两点,
两点,
当x=0时,y=![]() ,当y=0时,x=3,
,当y=0时,x=3,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
![]() ,即
,即![]() ,解得
,解得![]() ,
,
![]() ;
;
(2)![]() 抛物线
抛物线![]() 经过
经过![]() 两点,将
两点,将![]() 与
与![]() 代入得:
代入得:
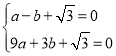 ,解得
,解得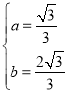 ,
,
![]() 抛物线解析式为
抛物线解析式为![]() ;
;
(3)![]() 轴,
轴,![]() ,
,
![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
![]() 的周长
的周长![]() ,
,
![]() 当
当![]() 有最大值时,其周长有最大值,
有最大值时,其周长有最大值,
![]() 点
点![]() 是直线
是直线![]() 上方抛物线上的一点,
上方抛物线上的一点,
![]() 设
设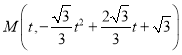 ,则
,则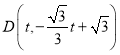 ,
,
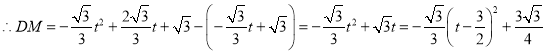 ,
,
![]() 当
当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() ,
,
此时![]() ,
,
即![]() 周长的最大值为
周长的最大值为![]() .
.

练习册系列答案
相关题目