��Ŀ����
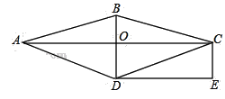
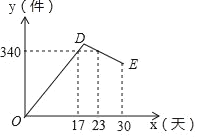
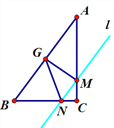
����Ŀ����ͼ����Rt��ABC�У���ACB��90�㣬BC��3��AC��4��G�DZ�AB���е㣬ƽ����AB�Ķ�ֱ��l�ֱ���ABC�ı�CA��CB�ڵ�M��N����CM��m.
��1����m��1ʱ������MNG�������
��2������G����ֱ��l�ĶԳƵ�Ϊ��G�����������G�� ǡ��������ABC���ڲ��������߽磩ʱ��m��ȡֵ��Χ��
��3����MNG�Ƿ����Ϊֱ�������Σ�����ܣ���������з���������m��ֵ��������ܣ���˵������.

���𰸡���1��![]() ����2��
����2��![]() ��m��4����3���ܣ�m��2��
��m��4����3���ܣ�m��2��![]()
����������������1����l//AB��֤��CMN����CAB�������Ƶ����ʼ��������MNG�ı�MN��MN���ϵĸߣ����������ε������ʽ���ɵó��𰸣�
��2�����ݵ�G����ֱ��l�ĶԳƵ�G���ֱ�����AB�ߡ�AC��ʱ��mֵ���������m��ȡֵ��Χ��
��3��������������ۣ���MNG�������ڽǷֱ�Ϊ90���������ɵó���.
��⣺��1����m��1ʱ��S��MNG��![]() ��
��![]() ��
��
��2������G����ֱ��l�ĶԳƵ�G������AB��ʱ��m��4��
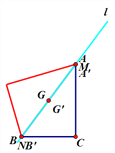
����G����ֱ��l�ĶԳƵ�G������AC��ʱ����M��AG�����е㣬
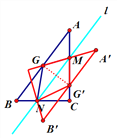
����AGG������ACB��
����AG����![]() ��
��
��CM��m��4��![]() ��
��![]() ��
��
���G��ǡ��������ABC���ڲ��������߽磩ʱ��![]() ��m��4��
��m��4��
��3����MNG��Ϊֱ����������
�ٵ���MGN��90��ʱ��
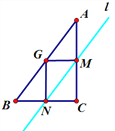
֤���ı���CMGNΪ������
��M��AC�����
��m��2��
�ڵ���GMN��90��ʱ��
![]() ��
��![]() ��
��
m��![]() ��
��
�۵���GNM��90��ʱ��![]() ��
��![]() ��
��
m����![]() ���������⣬��ȥ����
���������⣬��ȥ����
��m��2��m��![]() ʱ����MNG��ֱ��������.
ʱ����MNG��ֱ��������.