Question

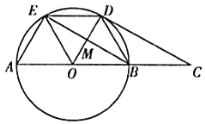
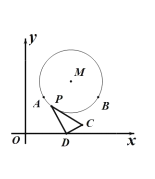
【题目】如图，在平面直角坐标系中，点、点在半径为的上，为上一动点，为轴上一定点，且当点从点逆时针运动到点时，点的运动路径长是(　　)

A.B.C.D.

Answer 1

【答案】A

【解析】

结合图形及tan∠DPC=tan30°=，且D为定点，分析动点P与动点C运动具有相关性，其运动的路径均为圆弧，长度比为对应线段的比，求出点P的运动弧长即可求解．

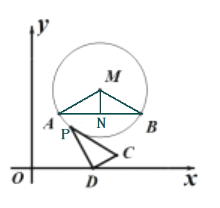
解：连接MA，MB，AB，过点M作AB的垂线交AB于N，则AN=BN=AB=，而MA=MB=，

在直角三角形AMN中，∵sin∠AMN=，

∴∠AMN=60°，故∠AMB=120°，

点P在圆上从点逆时针运动到点时，其所走的弧长为，

在PDC中，，故tan= ，且结合图形及P、C两点的相关性，知P、C的运动路径均为圆弧，且路径长度比为其对应得线段的比，即为，故点C的运动路径长为：．

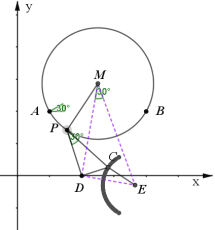
关于点C的路径简证：如图连接DM，以DM为直角边，构造一个直角三角形DME，使∠DME=30°，∠MDE＝90°，连接CE，则，而易知∠PDM=∠CDE，所以PDM∽CDE，故有，因此得到CE=PM=1，而通过构造知点E为定点，故点C的路径为以点E为圆心，1为半径的圆弧．

故选：A．