题目内容
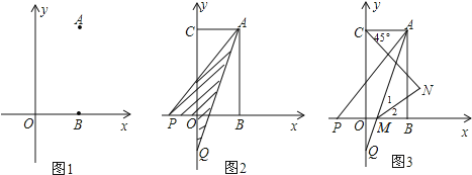
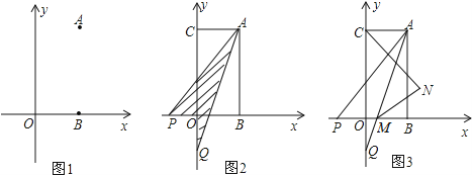
【题目】如图:已知在平面直角坐标系中点A(a,b)点B(a,0),且满足|2a-b|+(b-4)2=0.
(1)求点A、点B的坐标;
(2)已知点C(0,b),点P从B点出发沿x轴负方向以1个单位每秒的速度移动.同时点Q从C点出发,沿y轴负方向以2个单位每秒的速度移动,某一时刻,如图所示且S阴=![]() S四边形OCAB,求点P移动的时间;
S四边形OCAB,求点P移动的时间;
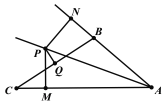
(3)在(2)的条件下,AQ交x轴于M,作∠ACO,∠AMB的角平分线交于点N,判断![]() 是否
是否![]() 为定值,若是定值求其值;若不是定值,说明理由.
为定值,若是定值求其值;若不是定值,说明理由.
【答案】(1)点A(2,4)、点B(2,0);(2)3s;(3)是定值,![]()
【解析】
(1)根据非负数的性质易得a=2,b=4,则点A的坐标为(2,4)、点B的坐标(2,0);
(2)设P点运动时间为t,则t>2,则P点坐标可表示为(2-t,0),Q点坐标表示为(0,4-2t),用待定系数法确定直线AQ的解析式为y=tx+4-2t,则可确定直线AQ与x轴交点坐标为(![]() ,0),根据题意得
,0),根据题意得![]() (
(![]() +t-2)×4+
+t-2)×4+![]() ×
×![]() ×(2t-4)=
×(2t-4)=![]() ×2×4,然后解方程求出t的值;
×2×4,然后解方程求出t的值;
(3)先根据角平分线定义得∠ACN=45°,∠1=∠2,再由AC∥BP得∠CAM=∠AMB=2∠1,然后根据三角形内角和定理得∠ACN+∠CAM=∠N+∠1,所以∠N=45°+∠1,再根据三角形外角性质得∠AMB=∠APB+∠PAQ,即∠APB+∠PAQ=2∠1,接着根据三角形内角和定理得∠AQC+∠OMQ=90°,利用∠OMQ=2∠1可得∠AQC=90°-2∠1,最后用∠1表示式子![]() 中的角,约分即可得到
中的角,约分即可得到![]() =
=![]() .
.
解:(1)∵|2a-b|+(b-4)2=0.
∴2a-b=0,b-4=0,
∴a=2,b=4,
∴点A的坐标为(2,4)、点B的坐标(2,0);
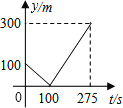
(2)如图2,设P点运动时间为t,则t>2,所以P点坐标为(2-t,0),Q点坐标为(0,4-2t),
设直线AQ的解析式为y=kx+4-2t,
把A(2,4)代入得2k+4-2t=4,解得k=t,
∴直线AQ的解析式为y=tx+4-2t,
直线AQ与x轴交点坐标为(![]() ,0),
,0),
∴S阴影=![]() (
(![]() +t-2)×4+
+t-2)×4+![]() ×
×![]() ×(2t-4),
×(2t-4),
而S阴=![]() S四边形OCAB,
S四边形OCAB,
∴![]() (
(![]() +t-2)×4+
+t-2)×4+![]() ×
×![]() ×(2t-4)=
×(2t-4)=![]() ×2×4,
×2×4,
整理得t2-3t=0,
解得t1=0(舍去),t2=3,
∴点P移动的时间为3s;
(3)![]() 为定值.理由如下:
为定值.理由如下:
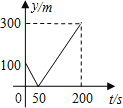
如图3,∵∠ACO,∠AMB的角平分线交于点N,
∴∠ACN=45°,∠1=∠2,
∵AC∥BP,
∴∠CAM=∠AMB=2∠1,
∵∠ACN+∠CAM=∠N+∠1,
∴45°+2∠1=∠N+∠1,
∴∠N=45°+∠1,
∵∠AMB=∠APB+∠PAQ,
∴∠APB+∠PAQ=2∠1,
∵∠AQC+∠OMQ=90°,
而∠OMQ=2∠1,
∴∠AQC=90°-2∠1,
∴![]() =
=![]() =
=![]() .
.