题目内容
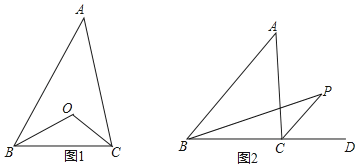
【题目】(1)如图1,△ABC中,BO平分∠ABC,CO平分∠ACB,∠A=56°,求∠BOC的度数;
(2)如图2,若点P为△ABC外部一点,PB平分∠ABC,PC平分外角∠ACD,先写出∠A和∠P的数量关系,并证明你的结论.
【答案】(1)∠BOC=118°;(2)∠A=2∠P,理由见解析
【解析】
(1)根据角平分线的定义和三角形的内角和定理求出∠OBC+∠OCB的值,再利用三角形的内角和定理求出∠BOC的值;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠PCD=∠P+∠PBC,根据角平分线的定义可得∠PCD=![]() ∠ACD,∠PBC=
∠ACD,∠PBC=![]() ∠ABC,然后整理得到2∠PCD=∠A.
∠ABC,然后整理得到2∠PCD=∠A.
解:(1)∵∠A=56°,
∴∠ABC+∠ACB=180°-∠A=124°,
∵BO、CO分别是∠ABC和∠ACB的角平分线,
∴∠CBO=∠ABO,∠ACO=∠BCO,
∴∠CBO+∠BCO=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×124°=62°,
×124°=62°,
∴∠BOC=180°-(∠CBO+∠BCO)=118°;
(2)∵BP、CP分别是∠ABC和∠ACB的角平分线,
∴∠ABC=2∠PBC,∠ACD=2∠PCD,
∴∠ACD-∠ABC=2(∠PCD-∠PBC),
∵∠A=∠ACD-∠ABC,∠P=∠PCD-∠PBC,
∴∠A=2∠P.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目