题目内容
【题目】阅读理解:
如图①,图形l外一点P与图形l上各点连接的所有线段中,若线段PA1最短,则线段PA1的长度称为点P到图形l的距离.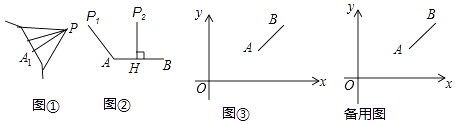
例如:图②中,线段P1A的长度是点P1到线段AB的距离;线段P2H的长度是点P2到线段AB的距离.
解决问题:
如图③,平面直角坐标系xOy中,点A、B的坐标分别为(8,4),(12,7),点P从原点O出发,以每秒1个单位长度的速度向x轴正方向运动了t秒.
(1)当t=4时,求点P到线段AB的距离;
(2)t为何值时,点P到线段AB的距离为5?
(3)t满足什么条件时,点P到线段AB的距离不超过6?(直接写出此小题的结果)
【答案】
(1)解:如图1,作AC⊥x轴于点C,
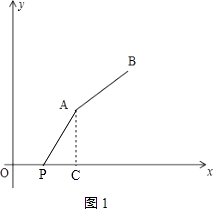
则AC=4、OC=8,
当t=4时,OP=4,
∴PC=4,
∴点P到线段AB的距离PA= ![]() =
= ![]() =4
=4 ![]() ;
;
(2)解:如图2,过点B作BD∥x轴,交y轴于点D,
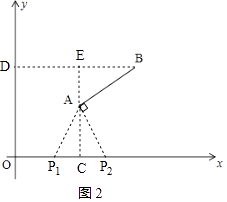
①当点P位于AC左侧时,∵AC=4、P1A=5,
∴P1C= ![]() =
= ![]() =3,
=3,
∴OP1=5,即t=5;
②当点P位于AC右侧时,过点A作AP2⊥AB,交x轴于点P2,
∴∠CAP2+∠EAB=90°,
∵BD∥x轴、AC⊥x轴,
∴CE⊥BD,
∴∠ACP2=∠BEA=90°,
∴∠EAB+∠ABE=90°,
∴∠ABE=∠P2AC,
在△ACP2和△BEA中,
∵ 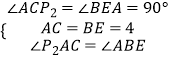 ,
,
∴△ACP2≌△BEA(ASA),
∴AP2=BA= ![]() =
= ![]() =5,
=5,
而此时P2C=AE=3,
∴OP2=11,即t=11;
(3)解:如图3, 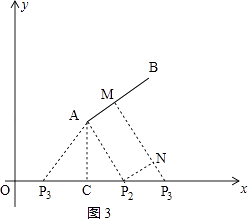
①当点P位于AC左侧,且AP3=6时,
则P3C= ![]() =
= ![]() =2
=2 ![]() ,
,
∴OP3=OC﹣P3C=8﹣2 ![]() ;
;
②当点P位于AC右侧,且P3M=6时,
过点P2作P2N⊥P3M于点N,
则四边形AP2NM是矩形,
∴∠AP2N=90°,∠ACP2=∠P2NP3=90°,AP2=MN=5,
∴△ACP2∽△P2NP3,且NP3=1,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴P2P3= ![]() ,
,
∴OP3=OC+CP2+P2P3=8+3+ ![]() =
= ![]() ,
,
∴当8﹣2 ![]() ≤t≤
≤t≤ ![]() 时,点P到线段AB的距离不超过6.
时,点P到线段AB的距离不超过6.
【解析】(1)类比定义,过P向直线引垂线,垂足不在线段上,因此P到线段的距离就是PA,须引垂线构造直角三角形;(2)须分类讨论:①当点P位于AC左侧时②当点P位于AC右侧时;(3)模仿(2),分类讨论:①当点P位于AC左侧②当点P位于AC右侧,先计算临界点,即AP3=6和P3M=6.
【考点精析】本题主要考查了点到直线的距离和全等三角形的性质的相关知识点,需要掌握从直线外一点到这条直线的垂线段的长度叫做点到直线的距离;全等三角形的对应边相等; 全等三角形的对应角相等才能正确解答此题.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案【题目】某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过20m3时,按2元/m3计算;月用水量超过20m3时,其中的20m3仍按2元/m3计算,超过部分按2.6元/m3计算.设某户家庭月用水量xm3.
月份 | 4月 | 5月 | 6月 |
用水量 | 15 | 17 | 21 |
(1)用含x的式子表示:
当0≤x≤20时,水费为 元;
当x>20时,水费为 元.
(2)小花家第二季度用水情况如上表,小花家这个季度共缴纳水费多少元?
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下(x>6且x<14,单位:km):
第一次 | 第二次 | 第三次 | 第四次 |
x |
| x﹣5 | 2(6﹣x) |
(1)写出这辆出租车每次行驶的方向;
(2)求经过连续4次行驶后,这辆出租车所在的位置(结果可用x表示);
(3)这辆出租车一共行驶了多少路程(结果用x表示)?