题目内容
【题目】如图,曲线AB是顶点为B,与y轴交于点A的抛物线y=﹣x2+4x+2的一部分,曲线BC是双曲线y= ![]() 的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2017,m)与Q(2025,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂足为M、N,连结PQ,则四边形PMNQ的面积为( )
的一部分,由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2017,m)与Q(2025,n)均在该波浪线上,过点P、Q分别作x轴的垂线,垂足为M、N,连结PQ,则四边形PMNQ的面积为( ) 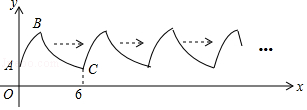
A.72
B.36
C.16
D.9
【答案】B
【解析】解:如图所示,A,C之间的距离为6, 2017÷6=336…1,故点P离x轴的距离与点P'离x轴的距离相同,
在y=﹣x2+4x+2中,当x=1时,y=5,即点P'离x轴的距离为5,
∴P'M'=5,
2025﹣2017=8,故点Q与点P的水平距离为8,
即M'N'=MN=8,点Q离x轴的距离与点Q'离x轴的距离相同,
由题可得,抛物线的顶点B的坐标为(2,6),故A,B之间的水平距离为6,且k=12,
∵点D与点Q'的水平距离为1+8﹣6﹣2=1,点C与点Q'的水平距离为1+2=3,
∴在y= ![]() 中,当x=3时,y=4,即点Q'离x轴的距离为4,
中,当x=3时,y=4,即点Q'离x轴的距离为4,
∴Q'N'=4,
∵四边形P'M'N'Q'的面积为 ![]() =36,
=36,
∴四边形PMNQ的面积为36,
故选:B.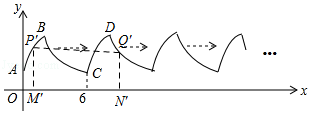
【考点精析】根据题目的已知条件,利用比例系数k的几何意义和二次函数的性质的相关知识可以得到问题的答案,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

【题目】本学期学校开展以“感受中华传统美德”为主题的研学活动,组织150名学生参观历史博物馆和民俗展览馆,每一名学生只能参加其中一项活动,共支付票款2000元,票价信息如下:
地点 | 票价 |
历史博物馆 | 10元/人 |
民俗展览馆 | 20元/人 |
(1)请问参观历史博物馆和民俗展览馆的人数各是多少人?
(2)若学生都去参观历史博物馆,则能节省票款多少元?