题目内容
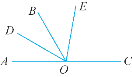
【题目】如图，O是直线AC上一点，OB是一条射线，OD平分∠AOB，OE在∠BOC内部，∠BOE＝
∠EOC，∠DOE＝70°，求∠EOC的度数．
【答案】80°
【解析】
设∠BOE=x°，则∠EOC=2x°，由∠DOE=70°，OD平分∠AOB知，∠AOD=∠DOB=70°﹣x°，再根据∠AOD+∠DOB+∠BOE+∠EOC=180°，列出关于x的方程求解即可．
解：如图，设∠BOE=x°，
∵∠BOE=
∠EOC，
∴∠EOC=2x°，
∵OD平分∠AOB，
∴∠AOD=∠DOB=70°﹣x°，
∵∠AOD+∠DOB+∠BOE+∠EOC=180°，
∴70°﹣x°+70°﹣x°+x°+2x°=180°，
∴x°=40°，
∴∠EOC=80°．
“点睛”本题主要考查角的计算及角平分线的定义，熟练掌握角平分线的定义及性质是解题的关键．
练习册系列答案
相关题目
