题目内容
【题目】如图,在![]() 中,
中,![]() 点
点![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,将
上,将![]() 沿
沿![]() 翻折,使得点
翻折,使得点![]() 落在点
落在点![]() 处,当
处,当![]() 时,则
时,则![]() ________________.
________________.
【答案】![]() 或
或![]()
【解析】
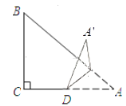
分两种情形分别求解,作DF⊥AB于F,连接AA′.想办法求出AE,利用等腰直角三角形的性质求出AA′即可.
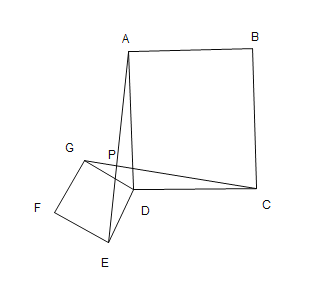
解:如图,作DF⊥AB于F,连接AA′.
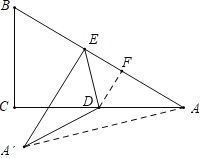
在Rt△ACB中,![]() ,
,
∵点D是AC的中点,AC=8,
∴![]() ,
,
∵∠DAF=∠BAC,∠AFD=∠C=90°,
∴△AFD∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵A′E⊥AB,
∴∠AEA′=90°,
由翻折不变性可知:∠AED=45°,
∴EF=DF=![]() ,
,
∴A′E=AE=![]() +
+![]() =
=![]() ,
,
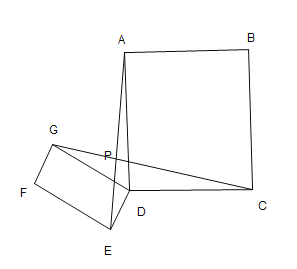
如图,作DF⊥AB于F,当 EA′⊥AB时,
同法可得AE=![]() ﹣
﹣![]() =
=![]() ,
,
∴A′E=AE=![]() .
.
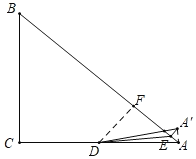
故答案为:![]() 或
或![]() .
.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目