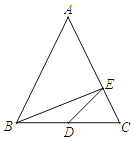
题目内容
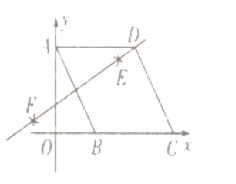
【题目】已知:点![]() 和
和![]() 是一次函数
是一次函数![]() 与反比例函数
与反比例函数![]() 图象的两个不同交点,点
图象的两个不同交点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 以及
以及![]() 分别与
分别与![]() 轴交与点
轴交与点![]() 和点
和点![]() .
.
(1)求反比例函数![]() 的表达式;
的表达式;
(2)若![]() ,求
,求![]() 的取值范围。
的取值范围。
【答案】(1)y=![]() ;(2)k≥2或k≤-10.
;(2)k≥2或k≤-10.
【解析】
(1)将点A(-1,-4)代入反比例函数![]() ,即可求解;
,即可求解;
(2)根据反比例函数和一次函数的图象,分两种情况进行讨论当P在第一象限或第三象限时,即可得k的取值范围.
解:(1)将点A(-1,-4)代入反比例函数![]() ,
,
得m=4,
所以y=![]() ;
;
(2)当P在第一象限时,当PP′≥![]() MN时,过点A作AC⊥PP’于点C,交x轴于点B,如图1
MN时,过点A作AC⊥PP’于点C,交x轴于点B,如图1
∵MN∥PP′,AC⊥MN
∴△AMN∽△APP'
∴![]()
得P(2,2),
直线AP表达式为y=2x-2,
当PP′≥![]() MN时,k≥2;
MN时,k≥2;
当P在第三象限时,如图2, 当PP′≥![]() MN时,过点A作AC⊥P P′于点C,交x轴于点B,
MN时,过点A作AC⊥P P′于点C,交x轴于点B,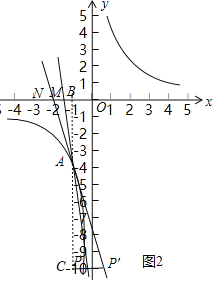
∵MN∥PP′,AC⊥MN,
∴△AMN∽△A PP′,
∴![]() ,
,
∴AC=6,
∴点P的纵坐标是-10,
把y=-10,代入y=![]() 中得x=-
中得x=-![]() ,
,
∴P的坐标为(-![]() ,-10),
,-10),
一次函数的解析式为y=-10x-14,
当PP′≥![]() MN时k≤-10.
MN时k≤-10.
所以k的取值范围是:k≥2或k≤-10.

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案【题目】如图1,线段AB及一定点C、P是线段AB上一动点,作直线CP,过点A作AQ⊥CP于点Q,已知AB=7cm,设A、P两点间的距离为xcm,A、Q两点间的距离为y1cm,P、Q两点间的距离为y2cm.小明根据学习函数的经验,分别对函数y1、y2随自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整:
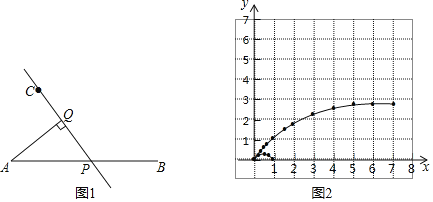
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1、y2与x的几组对应值.
x/cm | 0 | 0.3 | 0.5 | 0.8 | 1 | 1.5 | 2 | 3 | 4 | 5 | 6 | 7 |
y1/cm | 0 | 0.28 | 0.49 | 0.79 | 1 | 1.48 | 1.87 | 2.37 | 2.61 | 2.72 | 2.76 | 2.78 |
y2/cm | 0 | 0.08 | 0.09 | 0.06 | 0 | 0.29 | 0.73 | 1.82 |
| 4.20 | 5.33 | 6.41 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
(3)结合函数图象,解决问题:当△APQ中有一个角为30°时,AP的长度约为 cm.